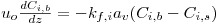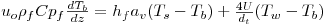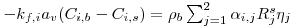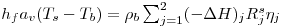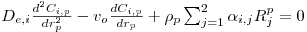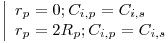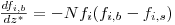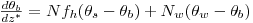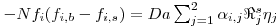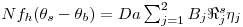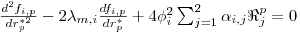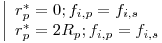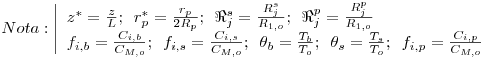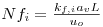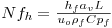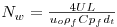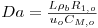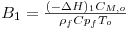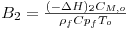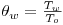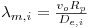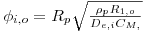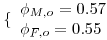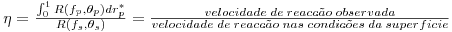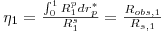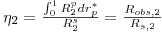1. Apresentação do sistema
2. Modelação matemática
CASO DE ESTUDO 2 - Oxidação do Metanol a Formaldeído num Reactor Catalítico de Leito Fixo
1. Apresentação do sistema
O caso de estudo reporta-se à reacção de oxidação parcial do metanol a formaldeído em fase gasosa, que tem lugar num reactor catalítico de leito fixo, tendo por base condições operatórias industriais. Quando a mistura reaccional contacta com o leito catalítico, são produzidos diversos compostos químicos para além do produto desejado, o que significa que para além da reacção desejada vão existir outras, designadas de reacções secundárias. Para o processo em análise, considerou-se que o sistema podia ser bem descrito considerando as seguintes reacções:
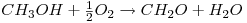 | (1) |
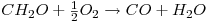 | (2) |
De acordo com a literatura, as velocidades das reacções (em mol kgp-1 s-1) são as indicadas na Tabela 1.
Tabela 1- Expressões cinéticas para o processo de oxidação parcial do metanol a formaldeído em catalisadores de Fe2O3 e MoO3.
| Referência | Cinética | Constantes |
| Dente et al. (1966) | 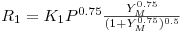 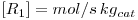
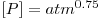
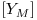 = fracção molar do metanol = fracção molar do metanol | 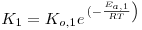
com:
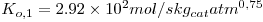
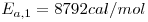 |
| Dente e Collina (1965) | 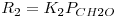 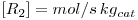
| 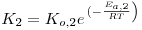
com:
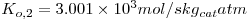
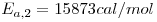 |
Ambas as reacções são fortemente exotérmicas, sendo a entalpia da reacção de conversão do metanol, eq. (1), igual a 158.68X103 J/mol e para a reacção secundária, eq. (2), de 233.21x103 J/mol.
De uma forma muito simplificada, representa-se na Fig. 1, um esquema das fases da produção do formaldeído.
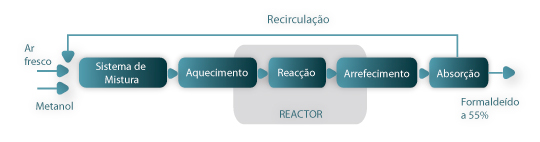
Figura 1- Diagrama simplificado do processo de fabrico do formaldeído a partir do metanol.
O ar fresco e a corrente de recirculação são misturados com o metanol e aquecidos até à temperatura a que a reacção ocorre. Após a reacção catalítica, há necessidade de se proceder ao arrefecimento da mistura reaccional antes da fase de absorção do formaldeído gasoso em água, obtendo-se no final, uma solução de 55% em peso. Como se pode concluir da Fig. 1, parte do aquecimento da mistura reagente e do arrefecimento do produto é feita no interior do reactor. Neste caso de estudo analisa-se o comportamento do reactor catalítico de leito fixo multitubular, o qual se baseia apenas no estudo de um tubo, já que se admite que todos têm o mesmo tipo de comportamento. Na Figura 2(a) indica-se um esquema simplificado que ilustra a configuração do reactor industrial. Na Figura 2(b) destaca-se um tubo com um comprimento total de 1.4 m, onde se pode observar a distribuição do catalisador e a parte do tubo sobre a qual o estudo de simulação vai incidir, ou seja, nas duas zonas intermédias do leito fixo, onde existe catalisador. A distribuição do catalisador por camadas distintas, é prática corrente na indústria, e está relacionada com a exotermicidade da reacção e com a actividade do catalisador. Ao colocar o catalisador distribuído desta forma, permite ter um leito menos activo na zona onde a concentração do reagente é maior.
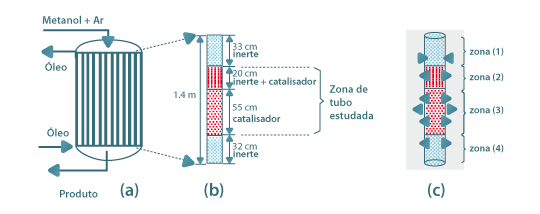
Figura 2- Representação esquemática: (a)- reactor multitubular industrial; (b) distribuição de catalisador nos tubos; (c)- sentido do fluxo de calor.
Com a Figura 2(c), pretende-se ilustrar o sentido do fluxo de calor em cada zona do tubo, podendo constatar-se que esta forma de distribuir o catalisador permite melhorar o processo de transferência de calor. Na zona (1) os tubos vão funcionar como permutador, permitindo que nas condições normais de operação, a temperatura aumente de 120ºC para 257ºC, pelo que se coloca aí apenas partículas sólidas inertes. À entrada da zona (2), a temperatura é sensivelmente igual à temperatura do fluido térmico (To=Tw=530 K) e como nesta zona existe catalisador (50% inerte+50% catalisador), inicia-se o processo reaccional. Atendendo a que a reacção é exotérmica, a temperatura no interior do tubo aumenta, tendo como consequência a inversão do fluxo de calor. O início da zona (2) é considerado também o início da coordenada axial do reactor, z=0, nos programas de simulação, e correspondem a 20 cm de tubo. Na zona (3), a actividade do leito aumenta (existe 100% de catalisador), o que faz com que a temperatura no interior do leito se eleve significativamente até se atingir o ponto quente, situação em que o calor produzido iguala o calor transferido para o exterior. A última parte do tubo, zona (4), tem apenas sólido inerte, funcionando novamente como permutador. Não se justifica ter catalisador nesta zona do tubo porque praticamente todo o metanol se consumiu nas zonas anteriores. Na Tabela 2, encontram-se os dados industriais que definem as características e as condições operatórias do sistema, necessárias para os estudos de simulação.
Tabela 2- Dados industriais do sistema de produção do formaldeído a partir do metanol.
| Características do Sistema |
| Reactor (1 tubo): | | | |
| Comprimento do reactor | L | 0.75 | mr |
| Diâmetro | dt | 0.021 | mr |
| Temperatura da parede | Tw | 530.0 | K |
| Porosidade do leito | εb | 0.5 | mvazios3/mr3 |
| Espessura dos tubos | ew | 1.75x10-3 | mr |
| Área específica da partíc./volume reactor | av | 1285 | mp2/mr3 |
| Massa específica do leito catalítico (100% cat.)* | ρb | 1100 | kgcat/mr3 |
| Razão de diâmetros reactor/partícula | dt/dpe | 9 | |
| Partícula: | | | |
| Diâmetro externo | de | 4x10-3 | mp |
| Diâmetro interno | di | 2x10-3 | mp |
| Altura | hp | 3.5x10-3 | mp |
| Diâmetro equivalente | dpe | 2.33x10-3 | mp |
| Área da superfície total dos poros | Sg | 10x103 | m2/kgcat |
| Área específica da partíc./volume da partíc. | Ap | 2.57x103 | mp2/mp3 |
| Massa específica | ρp | 2.20x103 | kgcat/mp3 |
| Porosidade | εp | 0.5 | mvazios3/mp3 |
| Tortuosidade | τp | 3.0 | |
| Raio médio dos poros | 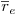 | 4.54x10-8 | mp |
| Semi-espessura da placa | Rp | 0.39x10-3 | mp |
| Velocidade intraparticular | vo | 0.013 | mf3/mp2 s |
| Condições de Operação à Entrada do Reactor |
| Pressão | Po | 1.40 | atm |
| Temperatura | To | 530.0 | K |
| Caudal molar total (por tubo) | Ft | 2.06x10-2 | mol/s |
| Percentagem molar de Metanol | YMo | 7.5 | % |
| Percentagem molar de Oxigénio | YOo | 10.18 | % |
| Percentagem molar de Formaldeído | YFo | 0.01 | % |
| Percentagem molar de Água | YAo | 2.50 | % |
| Percentagem molar de Monóxido de Carbono | YCOo | 0.75 | % |
| Percentagem molar de Inertes | Yio | 79.06 | % |
| Concentração de Metanol | CM,o | 2.414 | mol/mf3 |
| Velocidade superficial | uo | 1.85 | mf3/mr2s |
| Velocidade mássica | Go | 1.719 | kg/mr2s |
| Caudal volumétrico | Qvo | 6.41x10-4 | mf3/s |
| Tempo de passagem | τ | 0.203 | s |
| Propriedades Físicas das correntes de entrada e de saída industriais |
| Peso molecular (entrada; saída) | PM | 28.50; 27.47 | g/mol |
| Massa específica do fluido (entrada; saída) | ρf | 1.26; 1.76 | kgf/mr3 |
*- Para a zona do reactor, com 50% de catalisador e 50 % de inerte, a massa específica do leito, ρb, é 1100/2 kgcat/mr3.
::: Início :::
2. Modelação matemática
Neste caso de estudo, o comportamento estacionário do sistema pode ser analisado por duas abordagens distintas: modelo pseudo-homogéneo unidimensional (PH1D) e modelo heterogéneo unidimensional (HT1D).
Modelo pseudo-homogéneo unidimensional
O modelo PH1D corresponde à modelação mais simples que se pode utilizar para estudar um reactor tubular de leito fixo, e teve por base os seguintes pressupostos:
- não se distinguem as condições do fluido e do sólido, ou seja, desprezam-se os gradientes interparticulares (no filme) e intraparticulares (no interior do catalisador);
- a temperatura da parede é constante e igual à do fluido de arrefecimento;
- a resistência à transferência de calor entre o sistema e o exterior está concentrada num filme interno junto à parede;
- as propriedades físicas da mistura reaccional são constantes e foram calculadas nas condições de alimentação;
- a massa específica da mistura reaccional é constante e igual à da entrada, dado que sendo a maioria da mistura constituída por inertes, a variação do número de moles é desprezável;
- as concentrações, temperatura e pressão são constantes na direcção radial (modelo 1D);
- a contribuição da dispersão mássica e térmica na direcção axial são desprezadas;
- a velocidade do fluido é constante na direcção radial, ou seja, admite-se escoamento pistão;
O modelo matemático resulta do estabelecimento de dois balanços mássicos parciais ao metanol e ao formaldeído e um balanço de energia efectuados a um elemento de volume do reactor, pelo que as variáveis de estado são a concentração de metanol, CM, a concentração de formaldeído, CF, e a temperatura da fase fluida, T, as quais são indicadas na Tabela 3. Através da normalização das equações da Tabela 3, obtêm-se as equações da Tabela 4, das quais constam cinco parâmetros adimensionais, definidos na Tabela 5, onde se apresentam também os seus valores calculados nas condições de operação da Tabela 2. As concentrações, Ci, foram normalizadas pela concentração de metanol nas condições de entrada, CM,o, (fi=Ci/CM,o), a temperatura pela temperatura da alimentação, To, (θ=T/To), e as velocidades das reacções Rj, pela velocidade de reacção 1 nas condições de entrada, R1,o, tendo resultado as velocidades adimensionais 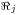
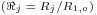 . A existência das duas zonas distintas do leito catalítico é contabilizada através do parâmetro ρb (massa específica do leito) incluído no parâmetro adimensional Da (número de Damkhöler). Sendo a massa específica do leito com catalisador puro (ρb=1100 kgcat/mr3, Tabela 2) dupla daquela que corresponde ao leito diluído com 50% de inerte, o número de Damkhöler na segunda zona será também duas vezes superior ao da primeira zona onde há diluição do catalisador.
. A existência das duas zonas distintas do leito catalítico é contabilizada através do parâmetro ρb (massa específica do leito) incluído no parâmetro adimensional Da (número de Damkhöler). Sendo a massa específica do leito com catalisador puro (ρb=1100 kgcat/mr3, Tabela 2) dupla daquela que corresponde ao leito diluído com 50% de inerte, o número de Damkhöler na segunda zona será também duas vezes superior ao da primeira zona onde há diluição do catalisador.
Tabela 3. Equações do modelo pseudo-homogéneo, unidimensional em estado estacionário.
Balanço Mássico Parcial
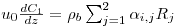 | (3) |
Balanço Energético
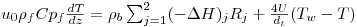
com: j= nº da reacção i= metanol; formaldeído | (4) |
| Condições iniciais: z=0 ; Ci=Ci,o ; T=To | (5) |
Tabela 4- Equações normalizadas do modelo pseudo-homogéneo, unidimensional em estado estacionário, PH1D.
Balanço Mássico Parcial
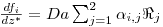
| (6) |
Balanço Energético
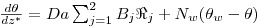
com: j= nº da reacção i= metanol; formaldeído | (7) |
| Condições Iniciais: z*=0 ; fi=Ci,o/CM,o ; θ=To/To | (8) |
Tabela 5- Parâmetros do modelo PH1D calculados a To=530 K e CM,o=2.414 mol/mf3.
| Número de Damkhöler * | | 1.04 |
| Elevação adiabática de temperatura adimensional da reacção 1 | | 0.72 |
| Elevação adiabática de temperatura adimensional da reacção 2 | | 1.07 |
| Número de unidades de transferência de calor para a parede | | 11.49 |
| Temperatura da parede adimensional | | 1.0 |
*- Para a segunda zona do reactor (100% de catalisador) Da=2x1.044
Modelo heterogéneo unidimensional
Dada a simplicidade do modelo anterior, há aspectos do comportamento do sistema que não ficam contemplados, pelo que se pode efectuar também a análise do sistema tendo em conta os gradientes entre as fases fluida e sólida. Para estabelecer o modelo heterogéneo unidimensional (HT1D) admitiram-se os seguintes pressupostos:
- contempla-se a heterogeneidade do meio, pelo que as condições da fase fluida e as das partículas de catalisador são distintas;
- o catalisador industrial tem a forma de anéis perfurados, Fig. 3(a). No entanto, nos estudos de simulação admitiu-se a geometria de placa plana, que corresponde a uma maior simplicidade das equações do modelo;
- a analogia entre as partículas de catalisador com diferente forma geométrica baseou-se na igualdade do volume/área.
- a transferência de massa e energia entre as duas fases, é feita através de um filme gasoso que envolve a partícula de catalisador, como se esquematiza na Fig. 3(b);
- relativamente à partícula de catalisador, considera-se que existe apenas transporte de massa por difusão.
- atendendo ao baixo factor de termicidade de Prater, desprezam-se as resistências térmicas intraparticulares, pelo que se consideram as partículas isotérmicas encontrando-se estas à temperatura da superfície, a qual é superior à do leito, dado que a reacção é exotérmica. Esta é a situação representada na Fig. 3(b);
- apesar da existência de uma fase gasosa e uma sólida, o modelo estabelecido é contínuo, uma vez que se recorre a parâmetros de transporte médios efectivos;
- a temperatura da parede é constante e igual à do fluido de arrefecimento;
- a resistência à transferência de calor, entre o sistema e o exterior, está concentrada num filme interno junto à parede;
- as propriedades físicas da mistura reaccional são constantes e foram calculadas nas condições de alimentação;
- a massa específica da mistura reagente é constante e igual à da entrada, dado que a maioria da mistura é inerte, ou seja, a variação do número de moles é desprezável;
- as concentrações, temperatura e pressão são constantes na direcção radial;
- a contribuição da dispersão mássica e térmica na direcção axial é desprezada;
- o escoamento do fluido no interior do reactor é considerado pistão;
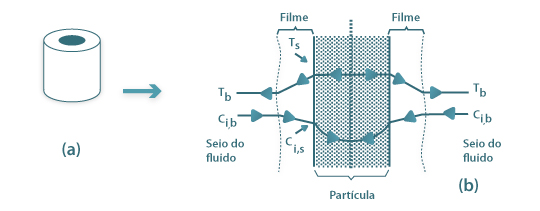
Figura 3- Partículas de catalisador: (a)- partícula industrial (anel perfurado); (b)- vista transversal da placa plana, esquematizando os gradientes de temperatura e concentração de um reagente i, para uma reacção exotérmica e com transporte de massa por difusão.
Como consequência destes pressupostos, resulta o modelo matemático da Tabela 6, o qual é constituído por dois balanços mássicos (um ao metanol e outro ao formaldeído) e um balanço térmico à fase fluida e ao filme gasoso em torno da partícula de catalisador, pelo que as variáveis de estado são: concentração do metanol na fase fluida, CM,b, concentração do formaldeído na fase fluida, CF,b, temperatura na fase fluida, Tb, temperatura na superfície do sólido, Ts, concentração do metanol na superfície do sólido, CM,s, e concentração do formaldeído na superfície do sólido CF,s. Para contabilizar a resistência à transferência de massa no interior do catalisador, que se considerou com comportamento isotérmico, efectuaram-se também dois balanços mássicos à partícula de catalisador, eqs.(14) e (15) da Tabela 6. Procedeu-se também à normalização das equações da Tabela 6, tendo resultado a Tabela 7, onde as concentrações foram normalizadas pela concentração do metanol à entrada, CM,o (fi=Ci/CM,o), as temperaturas pela temperatura de entrada, To (θ=T/To), as velocidades de reacção à superfície, Rjs, e nas condições da partícula, Rjp, foram normalizadas pela velocidade de reacção 1 nas condições de entrada, R1,o, tendo resultado as velocidades das reacções normalizadas, 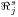 e
e 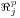 , respectivamente,
, respectivamente, 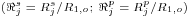 . O modelo matemático normalizado, é definido a partir dos parâmetros referidos na Tabela 8, cujos valores foram calculados nas condições da alimentação indicadas na Tabela 2.
. O modelo matemático normalizado, é definido a partir dos parâmetros referidos na Tabela 8, cujos valores foram calculados nas condições da alimentação indicadas na Tabela 2.
A velocidade intraparticular, v0, calculada para as condições de operação da Tabela 2 é 0.013 mf3/mp2s. Este valor para o Peclet mássico intraparticular é baixo e não introduziria grandes diferenças relativamente ao caso em que λm=0. Deste modo, as simulações interactivas contemplam apenas esta situação.
Tabela 6 - Equações do modelo heterogéneo, unidimensional em estado estacionário.
| Fase Fluida |
Balanço Mássico Parcial
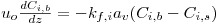
| (9) |
Balanço Energético
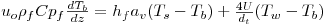
com i= metanol; formaldeído | (10) |
| Condições Iniciais: z=0 ; Ci,b=Ci,bo ; Tb=Tbo | (11) |
| Interface Fluido/Partícula |
Balanço Mássico Parcial
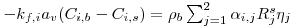 | (12) |
Balanço Energético
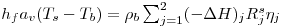
com: j= nº da reacção
i= metanol; formaldeído | (13) |
| Partícula de Catalisador |
Balanço Mássico Parcial
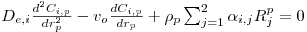
com: j= nº da reacção i= metanol; formaldeído | (14) |
Condições Fronteira:
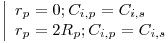
| (15) |
Tabela 7- Equações normalizadas do modelo heterogéneo, unidimensional em estado estacionário: HT1D
| Fase Fluida |
Balanço Mássico Parcial
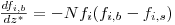
| (16) |
Balanço Energético
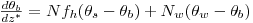
com: i= metanol; formaldeído | (17) |
| Condições Iniciais: z*=0 fi,b=Ci,bo/CM,o ; θb=Tbo/To | (18) |
| Interface Fluido/Partícula |
Balanço Mássico Parcial
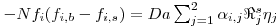
| (19) |
Balanço Energético
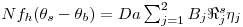
com: j= nº da reacção
i= metanol; formaldeído | (20) |
| Partícula de Catalisador |
Balanço Mássico Parcial
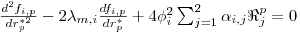
com: j= nº da reacção
i= metanol; formaldeído | (21) |
Condições Fronteira:
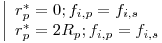 | (22) |
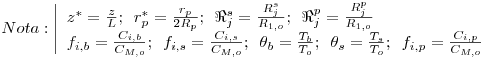
Tabela 8- Parâmetros dos modelos HT1D e HT1D dccalculados a To=530 K e CM,o=2.414 mol/mf3
| Número de unidades de massa transferidas no filme | 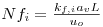
| i=M : 95.5
i=F : 100.4 |
| Número de unidades de calor transferidas no filme | 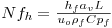
| 118.7 |
| Número de unidades de calor transferidas do fluido para a parede | 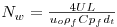
| 11.49 |
| Número de Damkhöler * | 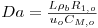
| 1.044 |
| Elevação adiabática de temperatura adimensional da reacção | 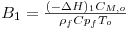
| 0.729 |
| Elevação adiabática de temperatura adimensional da reacção 2 | 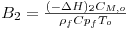
| 1.071 |
| Temperatura da parede adimensional | 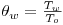
| 1.0 |
| Número de Peclet intraparticular do componente i ** | 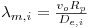
| 0 |
| Módulo de Thiele do componente i, relativo às condições de entrada | 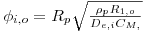 | 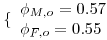 |
* - Para a segunda zona do reactor (100% de catalisador) Da=2x1.044; **- com λm,i=0, apenas o fluxo difusional está a ser considerado no modelo matemático.
Outro aspecto importante a referir, é a forma como os balanços mássicos às partículas de catalisador estão relacionados com os da fase fluida. De facto, não é possível integrar as eqs. (16) a (22) simultaneamente dado que envolvem variáveis independentes espaciais que não pertencem à mesma dimensão: z* é relativa à direcção axial do reactor, e rp* é relativa à direcção espacial da partícula. A ligação das equações tem como base o cálculo do factor de eficiência, o qual permite para cada posição axial, conhecer a velocidade de reacção observada nas partículas de catalisador, sendo definido da seguinte forma:
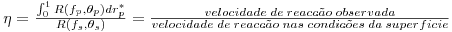
com: R(fp,θp)- velocidade de reacção na posição normalizada da partícula, rp* ;
R(fs,θs)- velocidade de reacção nas condições da superfície;
fp, fs - concentração normalizada, na posição rp* da partícula e na sua superfície;
θp- temperatura normalizada, na posição rp* da partícula, a qual é constante e igual à da superfície, θs (partícula isotérmica);
Uma vez que no sistema em análise são consideradas duas reacções, são calculados dois factores de eficiência, relativos a cada uma dessas reacções:
- factor de eficiência da reacção 1
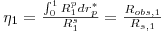 | (23) |
- factor de eficiência da reacção 2
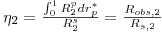 | (24) |
Devido às resistências à transferência de massa que têm de ser vencidas, a concentração do metanol no exterior da partícula é superior à do interior, pelo que a velocidade de reacção observada, Robs,1, é menor do que a velocidade da reacção nas condições da superfície, R1s. Assim, de acordo com a eq. (23), os limites do factor de eficiência da reacção 1 são: 0≤η1≤1. Por outro lado, o formaldeído produz-se no interior do catalisador e tem de se difundir para o exterior, sendo portanto, a velocidade da reacção observada, Robs,2, superior à velocidade nas condições da superfície, R2s. Assim, de acordo com a eq. (24), η2 é maior do que 1.
Bibliografia
M. M. J. Quina, Estabilidade Térmica em Reactores Catalíticos de Leito Fixo, Dissertação de Mestrado, Departamento de Engenharia Química - FCTUC, 312 pg, Coimbra (1997).
Dente, M., Collina, A., Pasquon, I., Verifica di un Reattore Tubolare per la Ossidazione del Metanolo a Formaldeide, La Chimica e L´Industria, 48(6), 581-588 (1966).
Dente, M., Collina, A., Cinetica dell´ossidazione del metanolo a formaldeide con catalizzatore a base di ossidi di Fe e Mo - Nota III, La Chimica e L´Industria, 47(8), 821-829 (1965).
::: Início :::





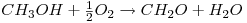
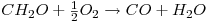
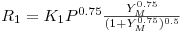
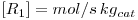
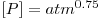
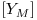 = fracção molar do metanol
= fracção molar do metanol 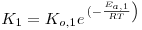
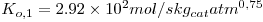
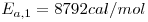
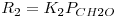
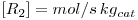
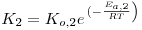
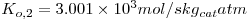
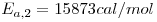


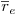
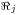
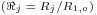 . A existência das duas zonas distintas do leito catalítico é contabilizada através do parâmetro ρb (massa específica do leito) incluído no parâmetro adimensional Da (número de Damkhöler). Sendo a massa específica do leito com catalisador puro (ρb=1100 kgcat/mr3, Tabela 2) dupla daquela que corresponde ao leito diluído com 50% de inerte, o número de Damkhöler na segunda zona será também duas vezes superior ao da primeira zona onde há diluição do catalisador.
. A existência das duas zonas distintas do leito catalítico é contabilizada através do parâmetro ρb (massa específica do leito) incluído no parâmetro adimensional Da (número de Damkhöler). Sendo a massa específica do leito com catalisador puro (ρb=1100 kgcat/mr3, Tabela 2) dupla daquela que corresponde ao leito diluído com 50% de inerte, o número de Damkhöler na segunda zona será também duas vezes superior ao da primeira zona onde há diluição do catalisador.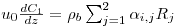
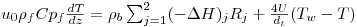
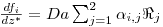
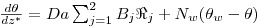
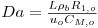
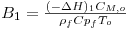
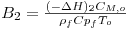
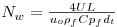
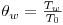

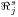 e
e 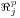 , respectivamente,
, respectivamente, 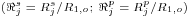 . O modelo matemático normalizado, é definido a partir dos parâmetros referidos na Tabela 8, cujos valores foram calculados nas condições da alimentação indicadas na Tabela 2.
. O modelo matemático normalizado, é definido a partir dos parâmetros referidos na Tabela 8, cujos valores foram calculados nas condições da alimentação indicadas na Tabela 2.