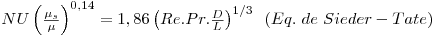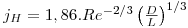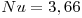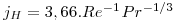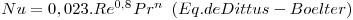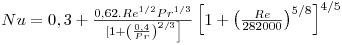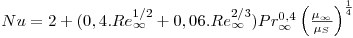O que é a TRANSFERÊNCIA DE CALOR? Como ocorre?
1.1 Condução de calor
1.2 Convecção de calor
1.3 Radiação térmica
1.4 Mecanismos Combinados
1.5 Resistências térmicas em série
1.6 Correlações empíricas
1.7 Bibliografia
O que é a TRANSFERÊNCIA DE CALOR? Como ocorre?
Energia térmica é a fracção da energia interna de um corpo que pode ser transferida devido a uma diferença de temperaturas. Esta fracção é composta pelas formas de energia microscópicas energia sensível e energia latente . Por exemplo, um corpo colocado num meio a uma temperatura diferente da que possui, recebe ou perde energia, aumentando ou diminuindo a sua energia térmica (ou interna, armazenada). Esta energia térmica transferida “para o” ou “do” corpo é vulgarmente designada por “Calor” e o processo é designado por Transferência de Calor. Não ocorrendo mudança de estado físico, a variação de energia interna sofrida por um corpo, de massa m, é igual ao calor transferido (Q) e pode ser estimada pela variação de temperatura ocorrida (ΔT), conhecido o seu calor específico, cP, como transcrito de uma forma simplista pela eq. 1. Havendo mudança de estado, a temperatura mantém-se constante, por exemplo na evaporação de uma massa m de um líquido, e o calor associado é calculado com recurso à eq. 2, onde ΔHvap é a entalpia específica de vaporização (obtida por subtracção da entalpia do líquido à entalpia do gás).
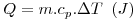
| (1) |
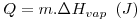
| (2) |
Existindo regiões no espaço a diferentes temperaturas (sendo esta diferença a driving-force, a causa, ou a força-motriz), ocorrerá transferência de calor no sentido das zonas onde a temperatura é mais baixa. Essa transferência pode ocorrer pelo mecanismo da condução, convecção e/ou radiação dependendo se ela se efectua através de sólidos ou de fluidos, entre sólidos separados por fluidos, entre fluidos separados por uma superfície sólida ou ainda entre superfícies sólidas entre as quais não existe matéria (vácuo absoluto) - Fig. 1.
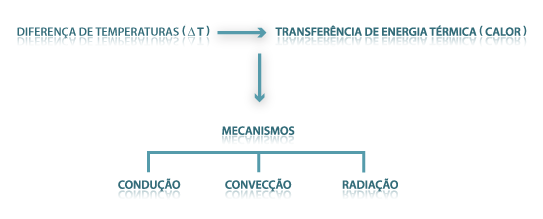

Fig 01: Modos de transferência de calor: radiação nas mãos, condução na tenaz e convecção no ar, o qual aquece ao percorrer o interior do tubo do recuperador de calor.
Muitas ocorrências do dia-a-dia envolvem transferência de calor (Fig. 2): arrefecimento do café numa chávena, favorecido pelo sopro sobre a sua superfície, aquecimento de água numa chaleira, a utilização de garrafas-termos para evitar o rápido arrefecimento de líquidos quentes, arrefecimento de alimentos no frigorífico ou o seu aquecimento num forno eléctrico, o arrefecimento do radiador do carro pelo ar ambiente circulante; no conforto humano refira-se os sistemas de ar condicionado, o aquecimento central, os aquecedores a óleo, o aquecimento do ar por meio de uma lareira, o isolamento de casas (com placas de poliuretano, esferovite, corticite, ou simplesmente uma camada de ar entre duas camadas de tijolo), a utilização de vidros duplos em vez de vidros simples.

Fig. 2 - Exemplos de situações diárias onde ocorre transferência de calor.
::: Início :::
1.1 Condução de calor
O mecanismo da Condução de calor está associado à transferência de calor efectuada ao nível molecular, por transferência de energia sensível. As partículas mais energéticas (que se encontram em locais onde se regista uma maior temperatura) transferem parte da sua energia vibracional, rotacional e translaccional por contacto com outras partículas contíguas menos energéticas (que se encontram a uma menor temperatura) as quais recebem essa energia. Essa transferência é efectuada, portanto, no sentido das temperaturas menores, ou seja, no sentido do gradiente (dT/dx) negativo (Fig. 3). Ocorre em gases, líquidos ou sólidos. Nos fluidos (especialmente nos gases, onde existem menores forças de coesão) surgem ainda colisões entre as partículas. Nos sólidos metálicos os electrões livres favorecem esse processo. A lei fundamental que descreve a condução térmica é a lei de Fourier (Joseph Fourier, 1768-1830) – eq.3. O calor transferido por unidade de tempo, ou a velocidade de transferência de calor, na direcção x 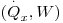 é proporcional à área de transferência perpendicular ao fluxo de calor (A=W×H, m2), e ao gradiente de temperaturas (dT/dx). A constante de proporcionalidade é uma propriedade física do material designada condutividade térmica (kT, W.m-1.K-1). O sinal negativo é necessário sempre que o gradiente seja negativo para que o calor, por convenção, tome um valor positivo.
é proporcional à área de transferência perpendicular ao fluxo de calor (A=W×H, m2), e ao gradiente de temperaturas (dT/dx). A constante de proporcionalidade é uma propriedade física do material designada condutividade térmica (kT, W.m-1.K-1). O sinal negativo é necessário sempre que o gradiente seja negativo para que o calor, por convenção, tome um valor positivo.
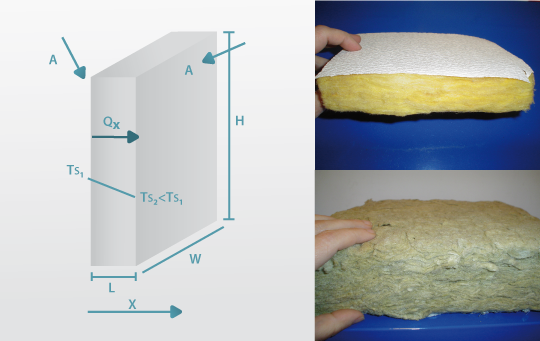
Fig. 3 - Transferência de calor através de uma parede. Para minimizar as perdas de calor para o exterior no Inverno ou as entradas de calor no Verão, as nossas habitações devem ter janelas e portas de vidro duplos e serem construídas com telhados e paredes duplas entre as quais se coloca um material isolante, como espumas de poliuretano, lã de vidro ou lã mineral.
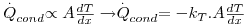
| (3) |
Por integração da eq.3 em estado estacionário (temperaturas constantes no tempo), obtém-se a eq. 4, considerando as condições fronteiras definidas na figura 3 e a condutividade térmica constante nesse intervalo de temperaturas:
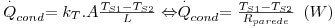
| (4) |
em que TS1 e TS2 são, respectivamente, as temperaturas na face esquerda e direita da parede e Rparede é a resistência térmica da parede, definida pela eq.5.
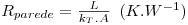
| (5) |
Se o material possuir uma condutividade térmica elevada, como é o caso dos metais (Tabela 1), a parede oferece pouca resistência à transmissão de calor por condução, e a queda de temperatura através da parede é baixa, isto é, se kT → ∞, Rparede → 0 , TS1 ≈ TS2. Diz-se nesse caso que o material é bom condutor. Pelo contrário, se o material possuir uma condutividade térmica baixa é um péssimo meio de propagação de calor e diz-se que é um isolante. Isolantes como a lã de rocha apresentada na Fig. 3 são usados no revestimento de condutas, tectos e paredes, para minimizar as trocas de calor com o exterior. Em geral, a condutividade térmica dos gases é menor do que a dos líquidos e esta menor que a dos sólidos.
Tabela 1 – Exemplos de valores de condutividade térmica para alguns materiais, a 300 K (Çengel, 2003; Holman, 2002; Incropera, de Witt, 2002).
Material | kT (W.m-1.K-1) |
Diamante | 2300 |
Cobre (puro)
| 401 |
Ferro (puro)
| 80 |
Vidro | 0,78 - 1,4
|
Madeira | 0,10 - 0,19
|
Água | 0,61 |
Ar | 0,026 |
Para as geometrias cilíndrica e esférica (como no caso de escoamento de fluidos no interior de condutas cuja parede está mais quente ou mais fria, ou em depósitos esféricos contendo fluidos armazenados), e considerando o fluxo de calor exclusivamente na direcção radial, a área de transferência não é constante ao longo do raio e as equações correspondentes são (considerando estado estacionário - temperaturas TS0 e TSi constantes no tempo):

Fig. 4 - Transferência de calor através de uma parede cilíndrica e esférica
::: Início :::
1.2 Convecção de calor
A existência de um fluido em movimento (líquido ou gás), acelera o processo de transferência de calor se um fluido mais frio (T∞), ficar em contacto com uma superfície mais quente (TS) como mostra a Fig. 5. Esta transferência dá-se em simultâneo com a transferência de calor ao nível molecular (por condução) sendo, no entanto, mais eficaz. A completa compreensão deste fenómeno requer o conhecimento da dinâmica do escoamento de fluidos, especialmente quando em contacto com superfícies. O movimento pode ser provocado por agentes externos, como por exemplo pela actuação de uma ventoinha, de um agitador ou de uma bomba centrífuga, ou por diferenças de densidade resultantes do próprio aquecimento do fluido (Fig. 6). No primeiro caso diz-se que a transferência de calor se processa por convecção forçada, enquanto no segundo por convecção natural ou livre. Assim, mesmo que um fluido se encontre em repouso (do ponto de vista macroscópico), a diferença de temperaturas gera diferenças de densidade no seio do fluido que poderão ser suficientes para induzir um movimento ascendente do fluido mais quente (sob a acção da gravidade). Em geral, a convecção de calor é definida de uma forma mais abrangente, associando-se o fenómeno da condução e o da transferência de calor em presença de movimento macroscópico do fluido. Apesar da complexidade matemática acrescida pelo movimento do fluido, especialmente quando esse movimento é aleatório, foi desenvolvido um modelo simples descrito pela eq. 10 para o cálculo da velocidade de transferência de calor que traduz o resultado conjunto destes dois fenómenos. Quando a velocidade do fluido diminui e tende para zero, a contribuição do movimento macroscópico do fluido perde importância face ao processo da condução.
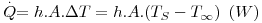
| (10) |
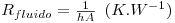
| (11) |
sendo h o coeficiente de transferência de calor (W.m-2.K-1), A, a área de transferência de calor perpendicular ao fluxo de calor e ΔT a driving-force, isto é, a causa para ocorrer a transferência de calor (p.e. pode ser (TS-T∞) em que TS é a temperatura de uma superfície e T∞ é a temperatura do fluido que a envolve, estando este mais frio - Fig. 5). A Tabela 2 apresenta algumas gamas de valores típicos para o coeficiente de transferência de calor.

Fig. 5 - Transferência de calor através de um fluido em movimento – o movimento pode ser provocado, por exemplo, por uma ventoinha – convecção forçada.
A eq. 10 é conhecida pela lei de Newton para o arrefecimento mas mais não é do que a equação de definição do coeficiente de transferência de calor. Este coeficiente não é uma propriedade física como a condutividade térmica na lei de Fourier e depende de algumas propriedades físicas do fluido, do tipo de movimento do fluido e da geometria da superfície que o fluido percorre. Por exemplo, se a agitação do fluido for elevada, o valor de h também será elevado e a resistência do fluido à transferência de calor, descrita pela eq.11, será muito pequena (diz-se que o fluido não oferece resistência à transmissão de calor sendo TS ≈ T∞). Como se pode ver na Tabela 2, o coeficiente de transferência de calor toma valores mais elevados quando ocorre mudança de fase e mais baixos no caso de convecção natural em gases, devido simultaneamente aos valores baixos da velocidade e da condutividade térmica do fluido. Este coeficiente pode ser determinado por métodos analíticos (em situações muito simples) ou através de correlações empíricas .
Tabela 2 - Gamas de valores típicos para o coeficiente de transferência de calor, h (Holman, 2002; Incropera, de Witt, 2002)
Tipo de convecção | h (W.m-2.K-1) |
Convecção natural em gases | 2 - 15 |
Convecção natural em líquidos | 50 - 1000 |
Convecção forçada em gases | 15 - 250 |
Convecção forçada em líquidos | 100 - 20000 |
Convecção com mudança de fase: ebulição e condensação | 2500 - 100000 |
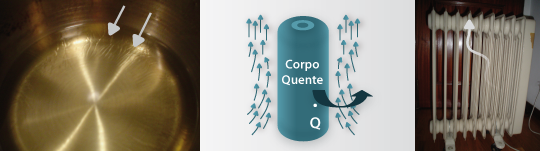
Fig 6 - formação de correntes de convecção natural (ou livre) provocadas pelo aquecimento do óleo numa frigideira ou do ar em torno de um corpo quente.
::: Início :::
1.3 Radiação térmica
Designa-se por radiação térmica, toda a energia radiante emitida na gama de comprimentos de onda 0,1 a 100 μm do espectro electromagnético (Fig. 7). Resulta da emissão e propagação de ondas electromagnéticas (ou fotões) por alteração na configuração electrónica de átomos e moléculas. Qualquer corpo com uma temperatura superior a 0 K emite energia radiante.
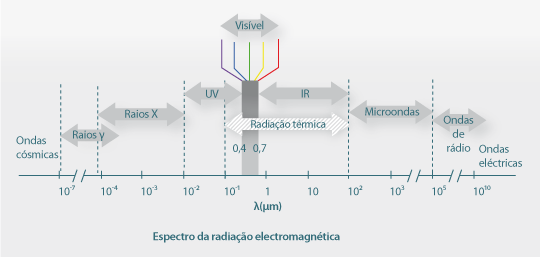
Fig. 7 – Espectro da radiação electromagnética.
A transferência de calor por radiação térmica ocorre através de sólidos, líquidos e gases e no vácuo, excepto nos sólidos e líquidos opacos à radiação térmica (que são a maioria). Como, em geral, os gases são pouco absorventes, a contribuição da radiação térmica para o calor total transferido não deve ser descurada nos cálculos de Engenharia quando se têm superfícies separadas por gases (como p.e. o ar). A energia radiante que um corpo emite é dada pela Lei de Stefan-Boltzmann (Josef Stefan 1835-1893, Ludwig Boltzmann 1844-1906) aplicada a um corpo real,
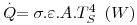
| (12) |
sendo σ=5,67×10-8 W.m-2.K-4 a constante de Stefan-Boltzmann, ε, a emissividade da superfície emissora (0<ε≤1), A, a sua área e Ts a sua temperatura absoluta (K). Como se vê na eq. 12, a energia emitida é proporcional à quarta potência da temperatura absoluta, pelo que a sua importância, relativamente aos outros mecanismos, aumenta com esta. Um corpo ideal (negro) emite a radiação máxima possível já que a sua emissividade é unitária. A Tabela 3 mostra alguns valores de emissividade de superfícies.
Tabela 3. Valores da emissividade de algumas superfícies a 300 K (Çengel, 2003; Incropera, de Witt, 2002)
Material | Emissividade, ε
|
Vegetação, solo, água, pele | 0,92 – 0,96 |
Asfalto | 0,85 – 0,93 |
Aço inox polido | 0,17 |
Ouro, prata ou cobre polidos | 0,018 – 0,035 |
O transporte de energia associado a este mecanismo é qualitativamente diferente dos mecanismos referidos nas secções anteriores (condução e convecção). Contudo, uma vez que todas as superfícies emitem radiação térmica, e esta será tanto maior quanto mais elevada for a temperatura, se um corpo emitir mais energia do que aquela que recebe proveniente das superfícies envolventes, a temperatura desse corpo diminuirá. Assim, para o cálculo da velocidade de perda ou ganho de energia, o que interessa é conhecer o resultado global da troca de energia radiante entre superfícies. Um exemplo, é a energia radiante trocada entre uma superfície de área A de um corpo pequeno à temperatura Ts e outra superfície vizinha à temperatura Tviz<TS que o envolve completamente, separadas por um fluido não absorvente.
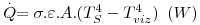
| (13) |
::: Início :::
1.4 Mecanismos Combinados
Num sólido opaco à radiação térmica a transferência de calor ocorre apenas por condução, enquanto num fluido opaco ela ocorre por convecção (a qual engloba a própria condução, como explanado acima). No vácuo apenas ocorre radiação. Nos sólidos, líquidos e gases não opacos, a transferência de calor ainda pode ocorrer por radiação, em paralelo à condução ou convecção. Diz-se que estamos perante mecanismos combinados. Segue-se um exemplo de aplicação (Çengel, 2003).
Determine o calor perdido por uma pessoa, por unidade de tempo, supondo que a sua superfície exterior se encontra a 29ºC, sendo a emissividade de 0,95. A pessoa encontra-se numa sala cuja temperatura ambiente é 20ºC (T∞) sendo a área do seu corpo de 1,6 m2 - figura 8. O coeficiente de transferência de calor entre a superfície exterior da pessoa e o ar pode considerar-se igual a 6 W.m-2.K-1.
Simplificações: desprezar a transferência de calor por condução através dos sapatos para o chão e o calor perdido por respiração e transpiração; supor que a temperatura das superfícies envolventes (paredes) é idêntica à temperatura ambiente (Tviz ≈ T∞0).
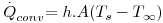
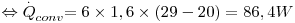
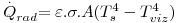
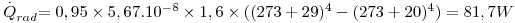
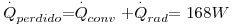
Desafio:
Supondo que no Verão e no Inverno o ar condicionado mantém a temperatura ambiente em 20ºC, explique porque sentimos frio no Inverno e calor no Verão sendo necessário adequar a quantidade de roupa vestida.
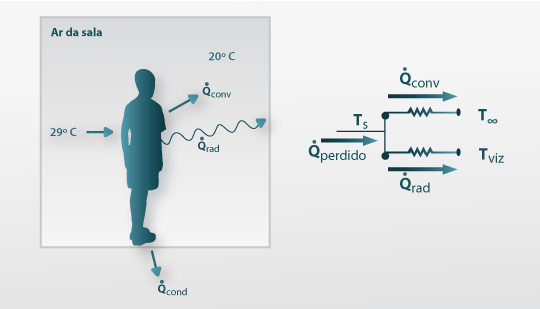
Fig. 8 – Transferência de calor por convecção e radiação, em paralelo.
Comentário: Quando ocorrem estes dois mecanismos em simultâneo é, por vezes, definido um coeficiente de transferência de calor combinado, h´, que os engloba como se só ocorresse transferência de calor por convecção. Assim, a expressão para o calor perdido, pode ser convertida em
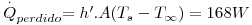
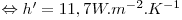
::: Início :::
1.5 Resistências térmicas em série
a) Geometria Plana
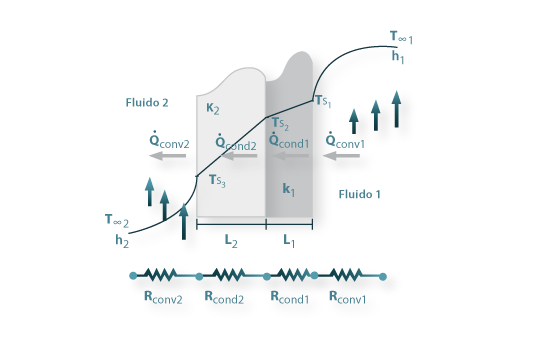
Fig. 9 - Transferência de calor entre dois fluidos separados por uma parede constituída por duas camadas de materiais diferentes.
Considere-se dois fluidos a diferentes temperaturas (T∞1 e T∞2) separados por uma parede plana composta como ilustra a Fig. 9. A transferência de calor é efectuada no sentido das temperaturas inferiores pelo mecanismo da condução nas paredes e por convecção nos fluidos. Considerando estado estacionário (T∞1 e T∞2 constantes no tempo) e a resistência de contacto entre superfícies desprezável, o fluxo de calor através de cada camada é o mesmo:
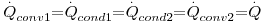
Usando as eq. (4 a 5) e (10 a 11), obtém-se:
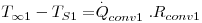
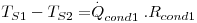
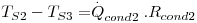
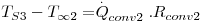
cuja soma é:
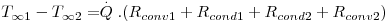
| (14) |
isto é, a velocidade de transferência de calor é a razão entre a diferença global de temperaturas e a resistência térmica total:
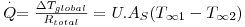
| (15) |
em que Rtotal é a resistência térmica total expressa por
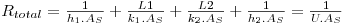
| (16) |
sendo U designado coeficiente global de transferência de calor.
b) Geometria Cilíndrica
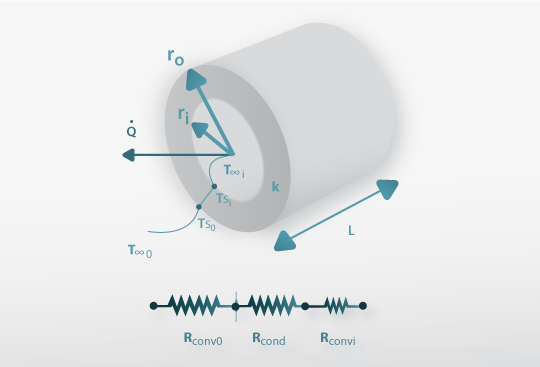
Fig. 10 - Transferência de calor entre dois fluidos separados por uma parede cilíndrica.
Considere-se agora dois fluidos, um quente e um frio, separados por uma parede cilíndrica como ilustra a Fig. 10. Em estado estacionário,
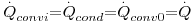
De (6) e (10), obtém-se:
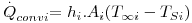
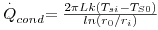
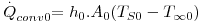
cuja soma é:
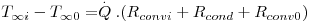
isto é, a velocidade de transferência de calor é a razão entre a diferença global de temperaturas e a resistência térmica total:
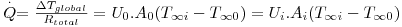
| (17) |
em que Ai=2πriL, A0=2πr0L sendo L o comprimento da conduta, Rtotal é a resistência térmica total expressa por
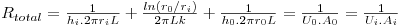
| (18) |
sendo U0 e Ui o coeficiente global de transferência de calor baseado na área da superfície externa e interna, respectivamente.
c) Exemplo de aplicação: perda de calor através de uma conduta de vapor com isolamento exterior (Çengel, 2003)
Uma conduta de ferro fundido (k=80 W.m-1.K-1) com o diâmetro interno de 5 cm e 2,5 mm de espessura de parede é usada para transportar vapor de água a 320ºC. A conduta está revestida por uma camada de lã de vidro (k=0,05 W.m-1.K-1) com 3 cm de espessura. A perda de calor para o ar ambiente a 5ºC ocorre por convecção natural e radiação, cujo coeficiente de transferência de calor combinado é 18 W.m-2.K-1. Supondo que não ocorre condensação e que o coeficiente de transferência de calor da superfície interna da conduta para o vapor é 60 W.m-2.K-1, determine:
(a) a perda de calor por unidade de comprimento da conduta;
(b) a queda de temperatura na parede da conduta e na camada do isolamento
Análise do problema e simplificações:
- Ocorre perda de calor através de uma conduta de vapor
- Há condução através da parede cilíndrica de ferro e através do isolamento, ambos de comprimento L; resistência de contacto é desprezada; k é ~constante
- Convecção forçada no interior (fluido quente) e natural no exterior (fluido frio)
- Radiação da sup. externa do isolamento para as paredes vizinhas – englobada no coeficiente transferência de calor
- Estado estacionário (T∞i e T∞0 constantes no tempo), transferência de calor unidireccional (r)
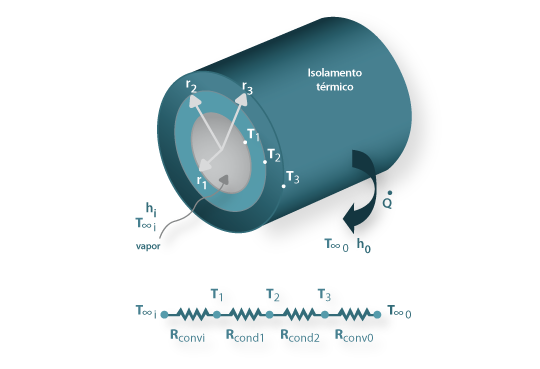
a)
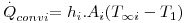
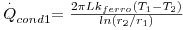
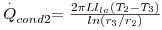
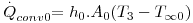
Ai=2πr1 L=0,157L m2 ;
A0=2πr3L=0,361L m2
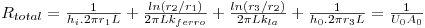
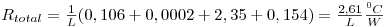
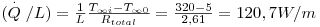
b)
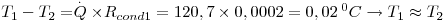
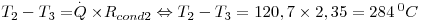
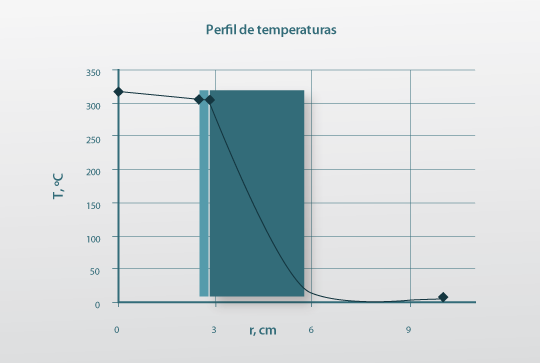
Comentários:
→ É o isolamento térmico que oferece a maior resistência à transferência de calor e, por isso, onde se verifica a maior queda de temperatura.
→ É comum desprezar Rcond na parede metálica face às outras Resistências; é de notar que devido à sua baixa resistência a queda de temperatura nesta parede á praticamente nula.
→ Na realidade, devido à perda de calor para o exterior, a temperatura do vapor (T∞i) não é constante ao longo do comprimento da conduta (pelo que Q/L também varia) embora a resistência total se mantenha.
::: Início :::
1.6 Correlações empíricas
Como já referido, o coeficiente de transferência de calor não é uma característica constante do fluido. Pelo contrário, depende, de uma forma complexa, não só das propriedades físicas do fluido (viscosidade, μ, massa volúmica, ρ, calor específico, cP, condutividade térmica, k) e da sua velocidade, u, mas também das dimensões da superfície por onde este se escoa, isto é, para o caso do escoamento no interior de uma conduta, h=f(μ, ρ, cP, k, u, D, L). A previsão teórica do valor de h, aplicando balanços de quantidade de movimento e térmico, só é possível ser efectuada para casos muitos simples. Por isso, h é determinado geralmente por via experimental. Contudo, a sua aplicabilidade é limitada ao sistema e condições estudadas.
Dado o elevado número de variáveis envolvidas no processo de transferência de calor é comum agrupar as variáveis sob a forma de números adimensionais e estabelecer correlações entre eles usando dados experimentais – por isso, são designadas correlações empíricas. Outra vantagem de se trabalhar com correlações empíricas, para além da redução do número de variáveis, é a sua aplicação em diversas situações/sistemas desde que estas se situem na sua gama de validade. Mesmo assim, os erros nas previsões dos valores dos coeficientes de transferência de calor, utilizando as correlações empíricas podem ascender a 25%.
Usando uma técnica de análise das dimensões das várias variáveis, é possível obter os números adimensionais característicos de um processo de transferência de calor por convecção forçada,neste caso aplicado ao escoamento no interior de uma conduta:
- o número de Reynolds, Re = ρu.D/μ que caracteriza o escoamento do fluido
- o número de Prandtl, Pr = μ.cP/k = ν/α que relaciona propriedades físicas do fluido, onde α=k/(ρ. cP) é a difusividade térmica, m2.s-1 e ν=μ/ρ é a viscosidade cinemática, m2.s-1.
- o número de Nusselt, Nu = h.D/k que representa o aumento da transferência de calor como resultado do movimento do fluido (“convecção”) relativamente à transferência de calor apenas ao nível molecular (condução)
- o factor geométrico D/L
Existem ainda outros números adimensionais possíveis que resultam da combinação destes:
- o número de Stanton para transferência de calor, Sth = Nu/(Re.Pr) = h/(ρ.u.cP)
- o número de Peclet para transferência de calor, Peh = Re.Pr = (ρ.u.cP.D)/k = u.D/α
- o número de Graetz, Gz = Re.Pr.D/L
- o factor de Colburn, jH = Sth.Pr2/3
Seguem-se alguns exemplos de correlações empíricas para o cálculo do coeficiente de transferência de calor no caso do escoamento de um fluido pelo interior de uma conduta circular de diâmetro interno D e comprimento L. As propriedades físicas do fluido são determinadas à temperatura média do fluido 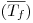 , entre a entrada (Tf1) e a saída da conduta (Tf2); se a viscosidade variar muito com a temperatura, deve ser utilizado o factor (μS/μ)0,14 a multiplicar Nu, sendo μS determinada à temperatura média da parede (TS). Na zona de entrada de uma conduta, e em virtude da resistência ao movimento do fluido, exercida pela parede, estabelece-se um perfil de velocidade, para além do perfil de temperatura se TS≠T∞. A velocidade e a temperatura variam, respectivamente, desde zero e TS junto à parede e um valor máximo no eixo central, sendo u e Tf a velocidade e a temperatura médias do fluido. Se TS>Tf, o fluido aquece e Tf2>Tf1. Os perfis de velocidade e temperatura vão-se desenvolvendo até atingirem uma forma constante ao fim de um comprimento designado comprimento de entrada hidrodinâmico, Lh, e térmico, Lt. Se o comprimento da conduta for superior a Lh e Lt, em simultâneo, diz-se que ambos os perfis estão completamente desenvolvidos.
, entre a entrada (Tf1) e a saída da conduta (Tf2); se a viscosidade variar muito com a temperatura, deve ser utilizado o factor (μS/μ)0,14 a multiplicar Nu, sendo μS determinada à temperatura média da parede (TS). Na zona de entrada de uma conduta, e em virtude da resistência ao movimento do fluido, exercida pela parede, estabelece-se um perfil de velocidade, para além do perfil de temperatura se TS≠T∞. A velocidade e a temperatura variam, respectivamente, desde zero e TS junto à parede e um valor máximo no eixo central, sendo u e Tf a velocidade e a temperatura médias do fluido. Se TS>Tf, o fluido aquece e Tf2>Tf1. Os perfis de velocidade e temperatura vão-se desenvolvendo até atingirem uma forma constante ao fim de um comprimento designado comprimento de entrada hidrodinâmico, Lh, e térmico, Lt. Se o comprimento da conduta for superior a Lh e Lt, em simultâneo, diz-se que ambos os perfis estão completamente desenvolvidos.
- Exemplo de correlações empíricas para Regime laminar (Re< 2000):
- Perfis de velocidade e temperatura em desenvolvimento (efeitos de entrada), sendo Ts constante e Nu>3,66; Lh<0.05Re.D; Lt<0.05Re.Pr.D
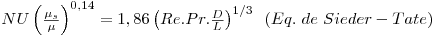
ou, transformando Nu no factor jH, obtém-se:
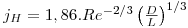
- Perfis de velocidade e temperatura completamente desenvolvidos (Lh>0.05Re.D; Lt>0.05Re.Pr.D), sendo Ts constante
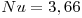
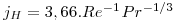
- Exemplo de correlações empíricas para Regime turbulento, tubos lisos, com perfis de velocidade e temperatura completamente desenvolvidos (Lh>10D; Lt>10D):
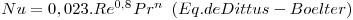
sendo n=0,4 (para aquecimento), n=0,3 (para arrefecimento), Re>104; L/D>10; 0,7<Pr<160.
- Exemplo de correlações empíricas para transferência de calor no caso de escoamento de um fluido em torno de cilindros
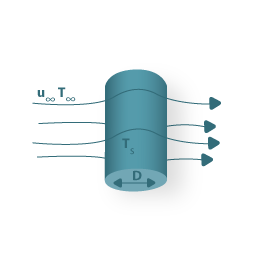
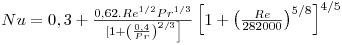
Re.Pr>0.2; 102<Re<107; propriedades avaliadas a T=½(TS+T∞); Nu=h.D/k; Re=ρ.u∞.D/μ.
- Exemplo de correlações empíricas para transferência de calor no caso de escoamento de um fluido em torno de esferas, cuja superfície está à temperatura TS
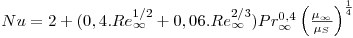
0,7<Pr<380; 3,5<ReD<8×104; Nu=h.D/k ; Re=ρ.u∞.D/μ ; propriedades avaliadas a T∞ excepto μS; é de notar que no caso da velocidade do fluido ser nula (repouso), Nusselt toma o valor 2: Re → 0 ⇒ Nu → 2.
Para ver outros exemplos de correlações empíricos, consultar a bibliografia ou o sítio http://www.cheresources.com/convection.shtml .
::: Início :::
1.7 Bibliografia
As referências bibliográficas e a bibliografia recomendada encontram-se no final da secção de Transferência de Massa.
::: Início :::





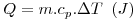
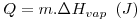



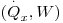 é proporcional à área de transferência perpendicular ao fluxo de calor (A=W×H, m2), e ao gradiente de temperaturas (dT/dx). A constante de proporcionalidade é uma propriedade física do material designada condutividade térmica (kT, W.m-1.K-1). O sinal negativo é necessário sempre que o gradiente seja negativo para que o calor, por convenção, tome um valor positivo.
é proporcional à área de transferência perpendicular ao fluxo de calor (A=W×H, m2), e ao gradiente de temperaturas (dT/dx). A constante de proporcionalidade é uma propriedade física do material designada condutividade térmica (kT, W.m-1.K-1). O sinal negativo é necessário sempre que o gradiente seja negativo para que o calor, por convenção, tome um valor positivo.
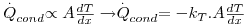
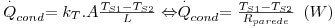
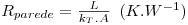

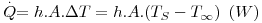
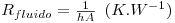



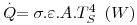
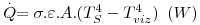
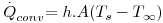
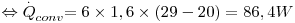
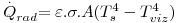
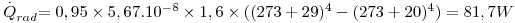
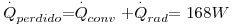

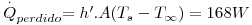
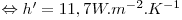

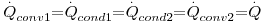
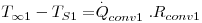
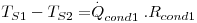
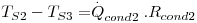
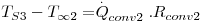
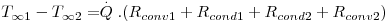
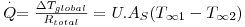
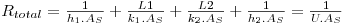

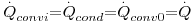
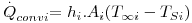
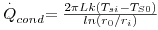
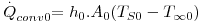
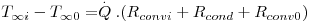
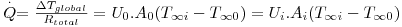
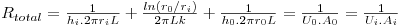

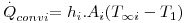
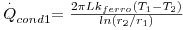
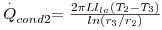
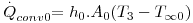
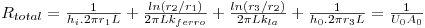
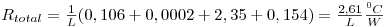
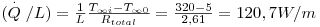
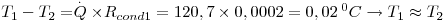
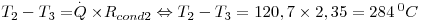

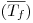 , entre a entrada (Tf1) e a saída da conduta (Tf2); se a viscosidade variar muito com a temperatura, deve ser utilizado o factor (μS/μ)0,14 a multiplicar Nu, sendo μS determinada à temperatura média da parede (TS). Na zona de entrada de uma conduta, e em virtude da resistência ao movimento do fluido, exercida pela parede, estabelece-se um perfil de velocidade, para além do perfil de temperatura se TS≠T∞. A velocidade e a temperatura variam, respectivamente, desde zero e TS junto à parede e um valor máximo no eixo central, sendo u e Tf a velocidade e a temperatura médias do fluido. Se TS>Tf, o fluido aquece e Tf2>Tf1. Os perfis de velocidade e temperatura vão-se desenvolvendo até atingirem uma forma constante ao fim de um comprimento designado comprimento de entrada hidrodinâmico, Lh, e térmico, Lt. Se o comprimento da conduta for superior a Lh e Lt, em simultâneo, diz-se que ambos os perfis estão completamente desenvolvidos.
, entre a entrada (Tf1) e a saída da conduta (Tf2); se a viscosidade variar muito com a temperatura, deve ser utilizado o factor (μS/μ)0,14 a multiplicar Nu, sendo μS determinada à temperatura média da parede (TS). Na zona de entrada de uma conduta, e em virtude da resistência ao movimento do fluido, exercida pela parede, estabelece-se um perfil de velocidade, para além do perfil de temperatura se TS≠T∞. A velocidade e a temperatura variam, respectivamente, desde zero e TS junto à parede e um valor máximo no eixo central, sendo u e Tf a velocidade e a temperatura médias do fluido. Se TS>Tf, o fluido aquece e Tf2>Tf1. Os perfis de velocidade e temperatura vão-se desenvolvendo até atingirem uma forma constante ao fim de um comprimento designado comprimento de entrada hidrodinâmico, Lh, e térmico, Lt. Se o comprimento da conduta for superior a Lh e Lt, em simultâneo, diz-se que ambos os perfis estão completamente desenvolvidos.