1. Crescimento celular
2. Coeficiente de Rendimento e Manutenção
3. Metabolismo endógeno
4. Cultura contínua. O Quimiostato
5. Agitação e Mistura
5.1 Tipos de agitadores
5.2 Chicanas
5.3 Mecanismos de mistura
5.4 Caracterização da mistura
5.5 Velocidade Mínima de Rotação
5.6 Potência de agitação sem arejamento
5.7 Potência de agitação com arejamento
6. Transferência de Massa
6.1 Determinação de KLa
6.2 Correlações para estimativa de KLa
7. Majoração de escala (scale-up)
7.1 Igual taxa de dissipação de energia específica (Pg/V)
7.2 Igualdade de KLa
7.3 Igual Velocidade de Corte (Shear) máxima
7.4 Igual tempo de mistura, tM
7.5 Igual Número de Reynolds, ReI
7.6 Comparação dos diferentes critérios de escalamento
1. Crescimento celular
Quando um meio de cultura é formulado e construído com os constituintes (nutrientes) adequados e é depois semeado com um inóculo de microrganismos estes vão reproduzir-se com uma dinâmica que é própria do micorganismo e da composição do caldo.
Uma única célula que seja inoculada num determinado instante t=0 irá desenvolver-se nesse meio e ao atingir a maturidade para se reproduzir dividir-se-á dando origem a duas células ao fim de um intervalo de tempo td. Cada célula-filha, por sua vez, dará origem também a duas células ao fim de novo intervalo de tempo td. E assim sucessivamente. Este intervalo de tempo td é designado “tempo de duplicação”. Ao fim de um tempo t haverá n=t/ td gerações. Assim, se num instante t0 houver N0 células então num outro instante t o número de células no meio de cultura será
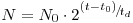 | (1) |
A base 2 não é a mais conveniente para os cálculos e a base “e” de Napier, dos logaritmos naturais, é mais recomendável. Então no mesmo instante, t, o número N de células será
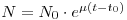 | (2) |
Conclui-se daqui que μ,designado “taxa específica de crescimento” está relacionado com os tempo de duplicação pela relação seguinte:
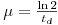 | (3) |
Uma medida mais adequada do que o número de células referido a uma unidade de volume será a concentração de biomassa, X, expressa em unidades de massa pró unidade de volume. Então a taxa volumétrica de crescimento (rX) num dado instante depende da taxa específica de crescimento e da concentração de biomassa nesse instante:
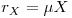 | (4) |
Num reactor descontínuo (sem qualquer fluxo de entrada e de saída) a concentração de biomassa varia apenas devido ao crescimento e se, do ponto de vista hidrodinâmico, houver mistura perfeita então o balanço de massa é simplesmente
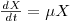 | (5) |
Em determinadas condições o parâmetro μ é constante e esta equação pode ser integrada para dar a quantidade de biomassa X em qualquer instante, t, sendo X0 a concentração de biomassa no instante t0=0:
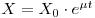 | (6) |
Contudo, a velocidade específica de crescimento depende das variáveis ambientais (T, pH, força iónica, nutrientes…) que o meio de cultura proporciona às células e da concentração de substrato limitante (aquele que mais rapidamente se esgota e que é, geralmente, a fonte de carbono). O modelo mais frequentemente usado para descrever a relação entre a velocidade específica de crescimento com a concentração de substrato limitante, com todas as outras variáveis mantidas constantes, foi proposto por Monod:
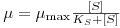 | (7) |
Nesta equação de Monod, KS é a “Constante de Monod” cujo valor é igual à concentração de substrato, [S]½, para a qual μ = ½μmax. Por sua vez, μmax é a velocidade específica máxima de crescimento que se poderia observar quando [S] → ∞.
::: Início :::
2. Coeficiente de Rendimento e Manutenção
O crescimento celular resulta da transformação do substrato em biomassa. A taxa de consumo de substrato, -rs,c, está pois relacionada com a taxa de crescimento celular, rx, através da relação
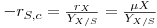 | (8) |
onde YX/S é o coeficiente de rendimento de biomassa relativamente ao substrato, significando a quantidade de biomassa obtida por unidade de massa de substrato consumido para o crescimento.
Contudo, as células vivas são, do ponto de vista termodinâmico, sistemas altamente estruturados cuja manutenção implica a dissipação de energia. Para restabelecer os níveis energéticos as células necessitam de incorporar substâncias ricas em energia que, para além da que é necessária para o crescimento, é também necessária para manutenção, i.e., para manter a composição iónica correcta (pressão osmótica) e para reposição de constituintes celulares, e ainda para outros processos vitais (processos de reposição de DNA, RNA e outras macromoléculas). A velocidade de consumo de substrato para essa manutenção por unidade de volume é proporcional à concentração de células (biomassa), e então
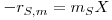 | (9) |
A constante de proporcionalidade, ms, é o “Coeficiente de Manutenção”.
Em tal situação a velocidade total de consumo de substrato por unidade de volume integra os dois processos, e será então
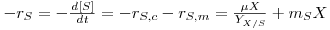 | (10) |
Com base nos dados directamente observáveis de [S] e X obtém-se um “coeficiente de rendimento observável”, YX/Sobs, inferior ao coeficiente teórico YX/S, tal que:
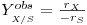 | (11) |
A diferença entre YX/Sobse YX/S resulta exactamente deste substrato consumido para a manutenção
::: Início :::
3. Metabolismo endógeno
Também a biomassa está sujeita a dois processos: o crescimento baseado no consumo de substrato e o decaimento endógeno. Esse decaimento da massa celular é em cada instante proporcional à concentração X de biomassa. A constante de proporcionalidade, kd, designa-se “constante de decaimento endógeno”
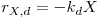 | (12) |
Considerações de ordem fisiológica indicam que dois factores independentes conduzem ao declínio da massa celular: i) as células perdem massa devido a metabolismo endógeno, e ii) lise, ambos caracterizados por constantes cinéticas, ke e kd0, respectivamente. A constante de decaimento endógeno é então a soma destas duas constantes
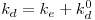 | (13) |
A taxa líquida de produção de biomassa será assim
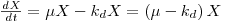 | (14) |
E a velocidade específica de crescimento resultante será
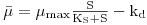 | (15) |
::: Início :::
4. Cultura contínua. O Quimiostato
Os processos contínuos permitem tirar maiores proveitos das designadas economias de escala. Neste tipo de processos as células são cultivadas até que se atinja uma pré-determinada concentração de biomassa nesse momento inicia-se o processo contínuo em que se alimenta o fermentador com caldo fresco e se retira uma quantidade de meio a uma taxa igual de modo a conservar o volume constante. Há duas estratégias diferentes geralmente usadas para cultivar microrganismos em processos contínuos em regime estacionário: turbidostato e quimiostato. Em qualquer dos casos estamos perante reactores contínuos perfeitamente agitados e o volume de suspensão no fermentador é constante.
No turbidostato os caudais de entrada e saída são iguais mas o caudal de entrada é ajustado de modo a manter constante a densidade de células. No quimiostato o volume de suspensão celular é constante mantendo iguais e constantes os caudais de entrada e saída: o tempo médio de permanência é constante e atinge-se o estado estacionário por auto-ajuste da densidade celular ao caudal de entrada. O quimiostato é, pois, um sistema auto-controlável enquanto o turbidostato (em que, pelo contrário, é o tempo médio de permanência que se ajusta à concentração de biomassa) requer uma estratégia de controlo muito mais complexa e não é, por isso, usado em escala comercial.
Na figura esquemática seguinte estão representadas as variáveis necessárias à análise da teoria do quimiostato: F é o caudal de alimentação igual ao caudal de saída, X e [S] são as concentrações de biomassa e de substrato, respectivamente, sendo o índice “0” relativo à alimentação, V é o volume útil do fermentador e rx é a velocidade de produção de biomassa por unidade de volume.
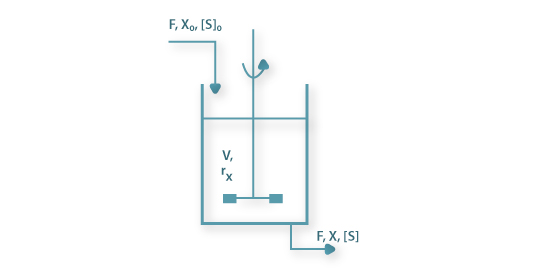
a) Balanço à biomassa
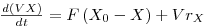 | (16) |
Dividindo por V, constante por definição de quimiostato, e considerando que rX=μX (equação 4), resulta
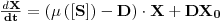 | (17) |
Nesta equação a “taxa de diluição”, D, é, por definição
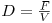 | (18) |
que mais não é que o inverso do tempo médio de permanência da suspensão de biomassa no fermentador em regime estacionário:
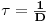 | (19) |
Da observação atenta da equação 17 pode concluir-se que
i) se 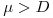 , então
, então 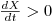 e a concentração X de biomassa aumenta até se atingir um novo estado estacionário com uma maior densidade celular.
e a concentração X de biomassa aumenta até se atingir um novo estado estacionário com uma maior densidade celular.
ii) se 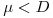 , então
, então 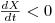 e a concentração X de biomassa diminui até se atingir um novo estado estacionário com uma menor densidade celular.
e a concentração X de biomassa diminui até se atingir um novo estado estacionário com uma menor densidade celular.
iii) se 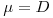 , então
, então 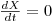 e a concentração X de biomassa mantém-se constante e o regime é estacionário.
e a concentração X de biomassa mantém-se constante e o regime é estacionário.
Supondo válido o modelo cinético de Monod e que kd « μ, resulta então que em regime estacionário (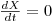 ):
):
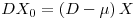 | (20A) |
ou
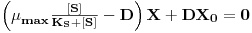 | (20B) |
e se a alimentação for estéril (X0 = 0) ter-se-á
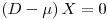 | (21) |
isto é,
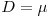 | (22) |
Conclui-se, pois, que a taxa específica de crescimento e, consequentemente, a concentração X de biomassa podem ser controladas por ajuste da taxa de diluição.
b) Balanço ao substrato
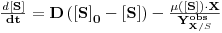 | (23) |
de onde se conclui que
i) se μ>D, então 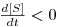 e a concentração [S] de substrato diminui até se atingir um novo estado estacionário com uma menor concentração [S].
e a concentração [S] de substrato diminui até se atingir um novo estado estacionário com uma menor concentração [S].
ii) se μ<D, então 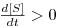 e a concentração [S] de substrato aumenta até se atingir um novo estado estacionário com uma maior concentração [S].
e a concentração [S] de substrato aumenta até se atingir um novo estado estacionário com uma maior concentração [S].
iii) se μ=D, então 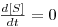 e a concentração [S] de substrato aumenta mantém-se constante e o regime mantém-se estacionário.
e a concentração [S] de substrato aumenta mantém-se constante e o regime mantém-se estacionário.
Supondo novamente válido o modelo cinético de Monod resulta então que em regime estacionário (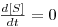 ):
):
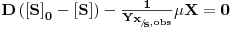 | (24A) |
ou, equivalentemente,
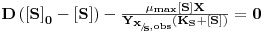 | (24B) |
que também implica que μ=D
Resolvendo o sistema de equações de balanço, com X0 = 0, e sendo [S]0 e D constantes, obtém-se as concentrações de biomassa e de substrato no estado estacionário
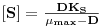 | (2 |
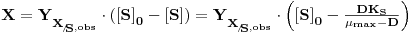 | (26) |
A concentração de biomassa no estado estacionério depende, pois, da concentração do substrato na alimentação e da taxa de diluição.
Representando graficamente estas funções tem-se a Figura 2 seguinte:
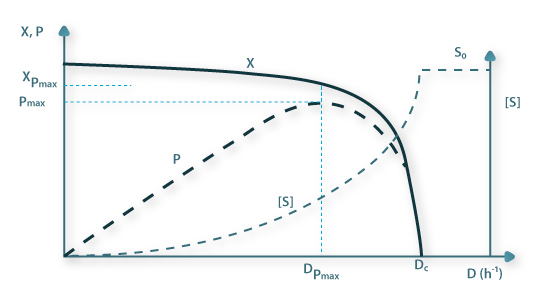
Figura 2: Produtividade e Concentrações da biomassa e do substrato em estado estacionário em função da taxa de diluição
Estas equações evidenciam, como também a Figura 2 mostra, que quando D → 0 se atinge o valor máximo de concentração de biomassa, Xmax, enquanto a concentração de substrato tem o seu valor mínimo, isto é, [S] → 0. Esta é uma situação que se aproxima do estádio final da cultura descontínua.
Para maiores valores de D as concentrações de biomassa e de substrato ajustam-se de acordo com as equações 25 e 26 que também evidenciam que D não pode ser superior a mmax. D atinge um valor crítico, Dc=mmax tal que, se for ultrapassado, a biomassa acaba sendo totalmente removida do fermentador, fenómeno que se designa vulgarmente por “wash-out”.
c) Produtividade
Para tirar maior partido dos investimentos que se fazem o fermentador deve operar em condições que maximizem a sua produtividade. No caso da produção de biomassa define-se produtividade pela relação
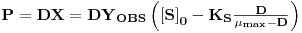 | (27) |
O valor da taxa de diluição (a que corresponde um caudal de alimentação) que maximiza a produtividade obtém-se derivando a equação 27 em ordem a D, e esse valor é
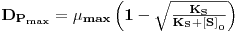 | (28) |
A correspondente concentração de biomassa é XPmax
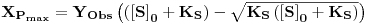 | (29) |
O valor da produtividade máxima é então (Figura 2)
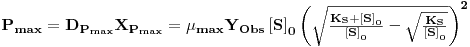 | (30) |
Exercício:
Neste desenvolvimento da teoria do quimiostato não se considerou nem o efeito do consumo de substrato para manutenção nem o metabolismo endógeno. Refaça esta análise considerando ambos os efeitos. Compare depois os seus resultados com os do simulador.
::: Início :::
5. Agitação e Mistura
Na análise feita da teoria do quimiostato formulou-se a condição de mistura perfeita. Essa condição implica a inserção agitadores no fermentador com funções diversas:
- promover a mistura de constituintes do meio de cultura reduzindo ou eliminando gradientes de concentração e de temperatura, assim tornando o meio mais homogéneo;
- manter os sólidos, em particular a biomassa, em suspensão;
- promover uma melhor transferência de massa gás-líquido, desintegrando as bolhas de ar e aumentando a área interfacial.
O conceito de mistura perfeita, ainda que fácil de concretizar em pequenos fermentadores laboratoriais, não é realizável em equipamento de escala comercial. Na Figura 3 está esquematizada a configuração standard de um reactor de mistura onde as dimensões dos órgãos internos estão relacionadas com a dimensão característica, DT, do reactor.
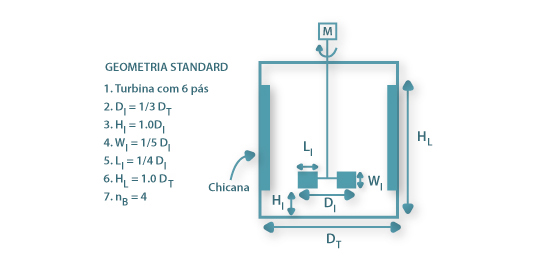
Figura 3: Características geométricas standard de um fermentador
A qualidade de mistura depende das características dos fluidos, do tipo e do modo de operação do agitador e da energia que é introduzida.
::: Início :::
5.1 Tipos de agitadores
A intensidade de agitação depende grandemente do tipo de agitador usado que deverá ser seleccionado em função da natureza do meio a agitar e da intensidade da mistura a impor.
Os agitadores podem dividir-se em duas classes: os de escoamento axial e os de escoamento radial. Os principais agitadores são do tipo hélice marinha (propellers), lâminas (“paddles”) verticais ou inclinadas e, sobretudo em fermentadores, turbinas de pás, e cada um deles ainda acomodam diversas variações e sub-tipos. Os agitadores do tipo propeller são de escoamento axial, usados para agitar meios de baixa viscosidade, rodam a velocidades elevadas e são também de menores dimensões (geralmente < 50 cm). As paddles rodam a velocidades baixas ou moderadas (20-150 rpm) e o seu diâmetro é da ordem de 50-80 % do diâmetro do tanque de mistura., o escoamento é radial, se as lâminas forem verticais, ou axiais, se as lâminas forem inclinadas. Mas a maior parte dos agitadores para caldos de fermentação são do tipo turbina de Rushton com 6 pás.

Figura 4: Principais tipos de agitadores para fluidos de baixa ou média viscosidade: (a) propeller; (b) paddle; (c) turbina de Rushton de 6 pás montadas
::: Início :::
5.2 Chicanas
As chicanas são usadas para evitar a formação de vórtices na agitação de líquidos de viscosidade reduzida, como o são os caldos de fermentação, quando o agitador está montado co-axialmente no fermentador. Em geral as chicanas, com uma largura igual a 1/10 do diâmetro do fermentador, são em número de quatro montadas verticalmente duas a duas em posição oposta junto à parede do fermentador; em muitos casos há um pequeno espaço entre a chicana e a parede.
A importância das chicanas advém da introdução de turbulência no líquido: o movimento do líquido sob a acção do agitador na ausência de chicanas mover-se-ia segundo linhas de corrente circulares em torno do eixo de agitação Figura 5 (a) e o grau de mistura entre diferentes camadas de líquido seria reduzido e formar-se-ia um vórtice forçado que introduziria ar no líquido e reduziria a potência transmitida ao líquido. Ao introduzir as chicanas as linhas de corrente são interrompidas, gera-se intensa turbulência e os vórtices e remoinhos são destruídos Figura 5 (b).
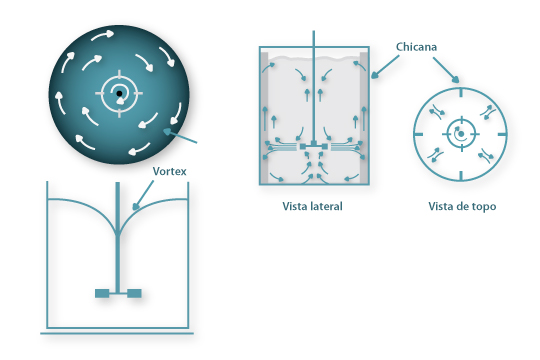
Figura 5: Perfis de escoamento num vaso (a) sem chicanas e (b) com chicanas com agitador montado co-axialmente.
::: Início :::
5.3 Mecanismos de mistura
O processo de mistura implica necessariamente o transporte dos componentes a misturar de modo a interpenetrarem-se, permutando material entre diferentes posições. Os processos físicos envolvidos nesse processo de mistura são:
- convecção (distribuição)
- turbulência (dispersão)
- difusão
As pás do agitador induzem um movimento circulatório, convectivo, no fluido (figura 5 (b)) que se distribui entre os dois grandes circuitos de convecção (loops), acima e abaixo das pás. Os diferentes componentes da mistura, dispersos em pequenos volumes na zona das pás, são levados e distribuem-se, assim, por todo o volume do vaso de mistura (fermentador). Este transporte convectivo, rápido em pequenos fermentadores laboratoriais, pode ser muito lento em fermentadores industriais de grandes dimensões. O resultado é uma uniformidade macroscópica mas ao nível molecular a mistura permanece altamente segregada.
Devido à elevada turbulência na zona das pás, movimento do fluido não se faz segundo linhas de corrente mas é aleatório, com direcções cruzadas. A sua energia cinética é concentrada em regiões de escoamento rotacional (eddies) de diversos tamanhos que co-existem dinamicamente, com os eddies de maiores dimensões a formarem-se na zona do agitador mas simultaneamente a quebrarem-se em eddies mais pequenos mas de maior energia cinética, e cada vez mais pequenos até não mais sustentarem movimento rotacional e a sua energia ser dissipada sob a forma de calor. O tamanho dos eddies mais pequenos é caracterizado por uma dimensão característica, o comprimento de Kolmogorov, também designado escala de mistura de Kolmogorov ou escala de turbulência, l. Sendo n a viscosidade cinemática e e (=P/rV)a taxa local de dissipação de energia por unidade de massa de fluido (igual, regime estacionário, à potência por unidade de massa transmitida pelo agitador ao fluido), então
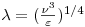
Dentro destes eddies a mistura ocorre por difusão, um mecanismo geralmente lento mas que, em virtude das pequenas distâncias de difusão, será ainda assim bastante rápido e conduz então a uma maior uniformidade molecular.
::: Início :::
5.4 Caracterização da mistura
Ao misturar os componentes de uma mistura, completamente segregados no início, o processo evolui para a homogeneidade passando por estádios de uniformidade crescente. Ao longo do tempo o volume mínimo de amostra com um grau de uniformidade representativo do todo o volume vai sendo cada vez menor e é uma medida da “escala de mistura”.
A caracterização da extensão de mistura depende, pois, da escala considerada e, embora na macro escala a mistura possa ser homogénea na micro-escala pode haver significativas heterogeneidades. Na escala considerada ter uma “mistura completa” significa que a probabilidade de um dado elemento ser detectado com a mesma concentração é a mesma qualquer que seja a posição considerada. A escala de avaliação a fazer depende naturalmente do processo e da aplicação em causa, mas para cada situação a questão da detecção põe restrições no que respeita às dimensões do detector (sensor): a escala de mistura deverá ser da ordem de 10% da dimensão característica do sensor.
A qualidade ou extensão da mistura pode ser caracterizada por dois parâmetros: a intensidade de mistura e o tempo de mistura. O estudo é feito normalmente recorrendo a técnicas de injecção de pulsos de um material que introduza uma propriedade facilmente mensurável (pH, condutividade eléctrica, densidade óptica, índice de refracção, radioactividade) numa ou em várias posições ao longo do tempo.
i) intensidade de mistura
O grau de mistura (ou complementarmente o grau de segregação) pode ser avaliado pela “intensidade de mistura” que mede o desvio em relação à mistura completa ideal na escala de mistura considerada, e pode ser quantificada pela expressão seguinte,
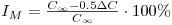 | (31) |
onde C∞ é a concentração do material de análise injectado no ponto de análise ao fim de um tempo prolongado, e a mistura considera-se completa quando ao fim de um tempo mais curto o valor medido se encontra num intervalo de ±0.5 DC em torno do valor C∞ de equilíbrio (Figura 6a).
ii) tempo de mistura
A selecção do agitador mais apropriado para uma dada aplicação, para numa “escala de mistura” definida atingir uma pré-estabelecida “intensidade de mistura”, requer também o conhecimento do “tempo de mistura”, isto é, de quão rápido é o processo de mistura até se atingir o grau de homogeneidade requerido. Recorrendo então à técnica de injecção de traços, o sensor da propriedade do material injectado colocado no ponto mais apropriado vai dar um sinal do tipo do da figura 6.
Os dados de concentração deverão ser normalizados, entre um valor inicial zero medido antes da adição do pulso a medir e um valor final estável medido no final do teste (tipicamente este valor final é registado ao fim de 30 segundos após a adição do traço), de modo a eliminar os efeitos dos diferentes ganhos dos sensores. A normalização obtém-se pela equação
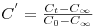 | (32) |
que quantifica o grau de mistura ou uma outra forma de definir a intensidade de mistura.
O tempo de mistura é então definido como sendo o tempo necessário para que a resposta normalizada do sensor se situe dentro de intervalo de ±5% do valor de equilíbrio final (Figura 7). Teremos nesse caso um valor particular de C’ conforme a equação 33.
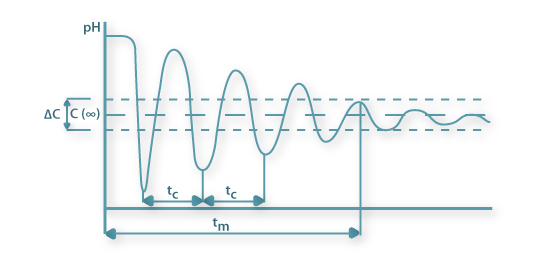
Figura 6a: Representação esquemática da relação da intensidade de mistura e do tempo de mistura em resposta a um pulso de ácido
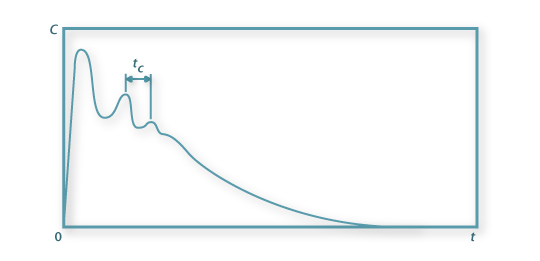
Figura 6b: Tipo de resposta de um sensor a um pulso injectado num Reactor contínuo com agitação mecânica
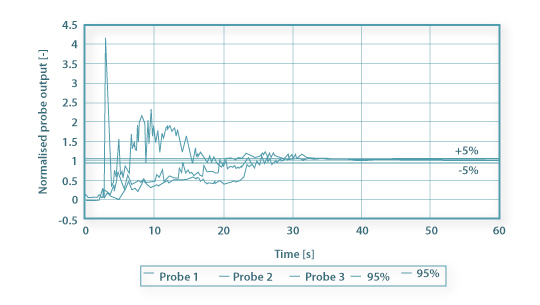
Figura 7: Respostas normalizadas de 3 sensores de condutividade.
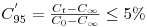 | (33) |
O tempo de mistura correspondente designa-se “tempo de 95% de mistura”, tM,95, e é o que geralmente se designa tempo de mistura tM. Pode estabelecer-se critérios mais exigente de qualidade de mistura e então para um qualquer grau de uniformidade, n, o tempo de mistura respectivo será tM,n tal que
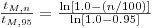 | (34) |
Na Figura 6 o espaço de tempo tC que medeia entre duas passagens do material do pulso pelo mesmo ponto onde se situa o sensor, designa-se “tempo de circulação” e está relacionado com o tempo de mistura tM. Em geral, . Num processo de mistura líquido-líquido num reactor de configuração standard equipado com uma turbina Rushton com 6 pás essa relação é, para regime turbulento,
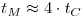 | (35) |
O tempo de mistura não é, porém, um valor de significado único e pressupõe a definição de uma escala de medida e de uma intensidade de mistura. O tempo de mistura será, pois, função da energia usada para agitar e misturar, e, portanto, do volume de líquido a agitar, das propriedades do líquido, e das características do agitador. Assim,
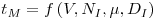 | (36) |
e pode ser correlacionado com o Número de Reynolds baseado no agitador, ReI, como se mostra na figura 8, sendo
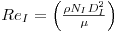 | (37) |
e
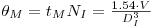 | (38) |
θM=tMNI é o tempo de mistura adimensional, que é constante em regime turbulento (ReI>104), mas que aumenta com a diminuição de ReI. NI é a velocidade de rotação do agitador, DI é o diâmetro do agitador e m é a viscosidade do fluido.
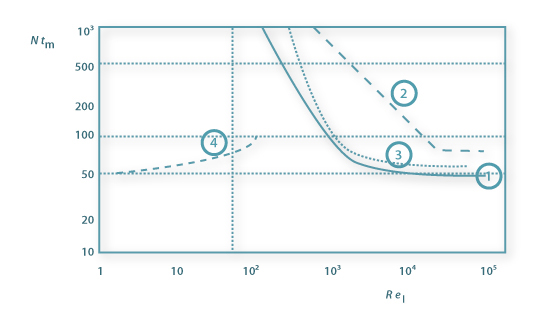
Figura 8: Tempo de mistura adimensional em função do Número de Reynolds baseado no impulsor: 1. turbina Rushton e chicanas; 2. hélice com chicanas; 3. agitador âncora; 4. agitador helicoidal.
Uma relação de tM,95 com a potência de agitação em regime turbulento, com um desvio padrão de ±10%, é
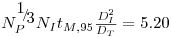 | (39) |
sendo DI e DT os diâmetros do agitador e do vaso, respectivamente, NI é a velocidade de rotação do agitador e NP é o “Número de Potência”.
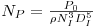 | (40) |
P0 é a potência transmitida pelo agitador ao fluido.
Em sistemas com arejamento o tempo de mistura e o tem de circulação aumentam relativamente a sistemas sem arejamento.
::: Início :::
5.5 Velocidade Mínima de Rotação
Em suspensões de partículas (as células e os flocos de células são partículas) há velocidade mínima do agitador que introduz a energia necessária para não deixar as partículas sedimentar. A equação de Zwietering pode ser usada para estimar essa velocidade mínima
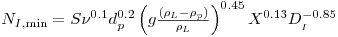 | (41) |
onde S é uma constante que depende da geometria do sistema e toma geralmente um valor entre 5 e 10; n é a viscosidade cinemática; dp e rL são o diâmetro e a massa específica da partícula (célula ou floco) e X é a concentração mássica da partícula.
5.6 Potência de agitação sem arejamento
A agitação de um fluido Newtoniano, sem arejamento, requer o fornecimento de energia a uma taxa que, entre outros factores, depende da velocidade de rotação e da dimensão do agitador e das propriedades do fluido.
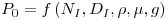 | (42) |
Recorrendo à análise dimensional, obtém-se
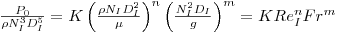 | (43) |
onde ReI é o Número de Reynolds e Fr é o Número de Froude.
Se outras variáveis fossem introduzidas na análise ter-se-ia uma expressão com muitos mais factores mas que em sistemas com semelhança geométrica se manteriam constantes e seria absorvidos pela constante K:
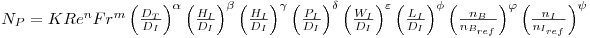
Introduzindo chicanas no sistema o expoente do Número de Froude é m = 0 e então
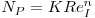 | (44 |
e
- regime turbulento (ReI > 104): n = 0
- regime laminar (ReI < 20): n = -1
Esta relação está graficamente representada na figura 9 para diferentes tipos de agitadores.
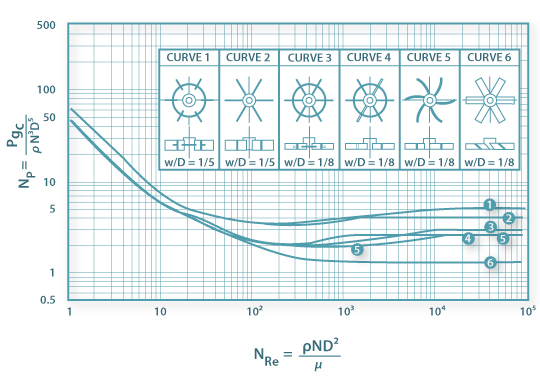
Figura 9: Relação entre o Número de Potência e o Número de Reynolds para diferentes tipos de agitadores
Considerando o que são NP e ReI tem-se que
- Regime laminar P0=KμNI2DI3
- Regime turbulento P0=KρNI3DI5
e, portanto, i) em regime laminar a potência absorvida pelo fluido depende da viscosidade do fluido mas não da sua massa específica, enquanto ii) em regime turbulento a potência transmitida ao fluido depende da massa específica do fluido mas não da sua viscosidade.
Em reactores de fermentação com configuração standard equipados com um turbina Rushton com 6 pás e com chicanas anti-vórtices o número de potência em regime turbulento (ReI > 5x103) será constante, NP = 5, e então
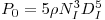 | (45) |
Em sistemas com vários andares o número de potência será proporcional ao número de andares.
5.7 Potência de agitação com arejamento
Quando em sistemas de cultivo aeróbio se introduz ar no sistema a potência consumida será menor não apenas porque a massa específica do sistema bifásico resultante é menor mas também, e sobretudo, por via da redução da resistência hidrodinâmica que as bolhas nas pás do agitador e a consequente redução da razão Pg/P0 de 1.0 para ~0.4 quando o “número de arejamento”, Na, varia de 0.035 até 0.05 correspondente a um aumento do caudal de ar, Qar.
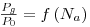 | (46) |
onde Na é o “Número de arejamento” ou “Número de escoamento”.
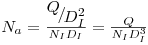 | (47) |
Várias correlações têm sido propostas para estimar a razão Pg/P0 em função de Na como a equação de Michel e Miller
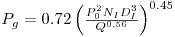 | (48) |
A razão Pg/P0 varia com o tipo de agitador, a escala do fermentador e a geometria do agitador e sistema de borbulhamento de ar.
6. Transferência de Massa
Em fermentações aeróbias a transferência de massa gás-líquido para oxigenação dos caldos processa-se vencendo várias resistências em série quando o oxigénio tem de se transferir das bolhas de ar até aos microrganismos. Contudo, o filme líquido em torno da bolha tem sido considerado como a principal e limitante resistência; por outro lado, resistências como as de interfaces não são fáceis de determinar de tal modo que todas as resistências são englobadas numa única global e assim o fluxo de oxigénio (OTR) é
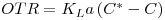 | (49) |
onde C* é a concentração de oxigénio na interface ar-líquido (aproximadamente a solubilidade do oxigénio), C é a concentração de oxigénio no todo do líquido, KL é o coeficiente global de transferência de massa e “a” é a área interfacial específica.
Os valores de KL e de “a” poderão ser estimados através de correlações ou medidos separada ou conjuntamente.
6.1 Determinação de KLa
A medição experimental de KLa pode ser feita por diferentes métodos
a) Método directo - balanço de massa global ao oxigénio
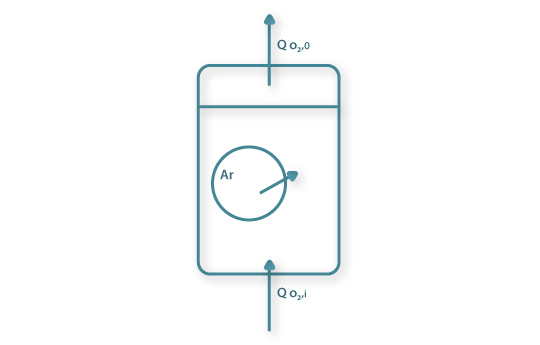
Por um balanço de massa ao oxigénio na fase gasosa tem-se
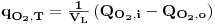 | (50) |
onde qO2,T é a quantidade de O2 transferida por unidade de tempo e unidade de volume de líquido à temperatura T, QO2, i e QO2,0 são as quantidade de O2 que entram e saem, respectivamente, por unidade de tempo no fermentador e VL é o volume de líquido. Considerando a equação de estado dos gases a equação anterior pode ser re-escrita e, então,
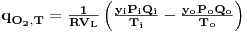 | (51) |
em que y, P e Q são a fracção molar de oxigénio no ar, a pressão total e o caudal de ar, respectivamente, e os índices i e o referem-se à entrada e à saída do fermentador, respectivamente. R é a constante dos gases perfeitos e T é a temperatura.
Das equações 49 e 51, e medindo C tira-se que
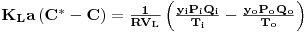 | (52) |
b) Desarejamento (Gassing-out) estático (estado não estacionário)
Na ausência de organismos respiratórios (sem consumo de oxigénio) extrai-se o oxigénio dissolvido no líquido do fermentador injectando N2 acompanhando o evoluir da concentração do oxigénio com um sensor polagrográfico. Quando essa concentração é suficientemente baixa, perto de 0% de saturação à temperatura do líquido, pára-se a injecção de N2 e inicia-se o borbulhamento de ar monitorizando e registando continuamente a evolução temporal da concentração de oxigénio. O aumento da concentração de oxigénio é devido apenas ao processo de dissolução no líquido. Estes dados serão depois tratados de acordo com os modelos seguintes.
O balanço de massa ao oxigénio num elemento de fluido traduz-se pela equação
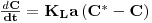 | (53) |
de onde, por integração, se tem
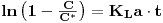 | (54A) |
Introduzindo os valores experimentais de C ao longo do tempo nesta equação e representando-os graficamente obtém-se uma recta cujo declive é o simétrico de KLa.
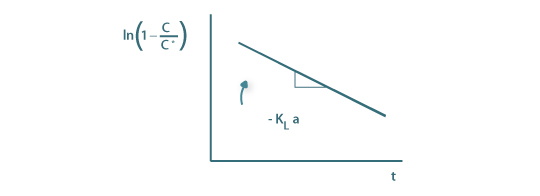
Figura 10a: Determinação de KLa segundo a equação 73A
Ou, equivalentemente,
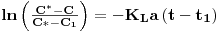 | (54B) |
com uma idêntica representação gráfica e o valor do declive é igual a –KLa.
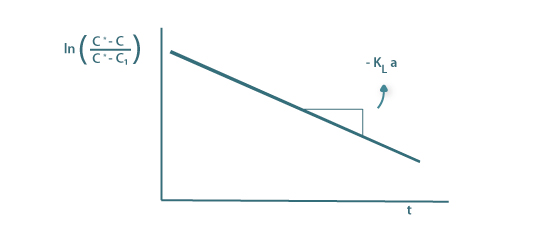
Figura 10b: Determinação de KLa segundo a equação 73B
iii) Desarejamento (Gassing-out) dinâmico
Numa cultura de organismos respiratórios em actividade num meio de cultura a concentração de oxigénio dissolvido resulta da quantidade que se transfere da corrente gasosa menos a que é consumida pelos microrganismos.
Do ponto de vista de determinação experimental fecha-se a alimentação do ar no instante t0 e a concentração de oxigénio diminui linearmente, a uma taxa constante, em resultado apenas do consumo pelos microrganismos. Quando a concentração do oxigénio dissolvido é baixa (mas acima da concentração crítica), no instante t1, abre-se de novo a alimentação do ar e a concentração de oxigénio aumenta a uma taxa que dependo da transferência e do consumo pelos microrganismos (Figura 11).
O balanço de massa ao oxigénio dissolvido num elemento de fluido é, então,
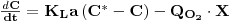 | (55) |
onde QO2 é a velocidade específica de consumo de oxigénio e X é a concentração de biomassa.
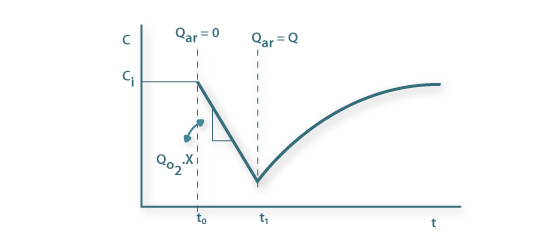
Figura 11: Representação esquemática da evolução temporal da concentração de oxigénio para determinação de KLa pelo método de desarejamento (gassing-out) dinâmico.
No intervalo de tempo de t0 a t1 a taxa de consumo de oxigénio é
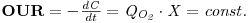 | (56) |
A partir do instante t1 a concentração de oxigénio obtém-se da equação 74 e, então
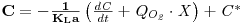 | (57) |
A representação gráfica de C em função de 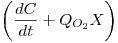 é ser uma recta com declive igual a
é ser uma recta com declive igual a 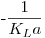
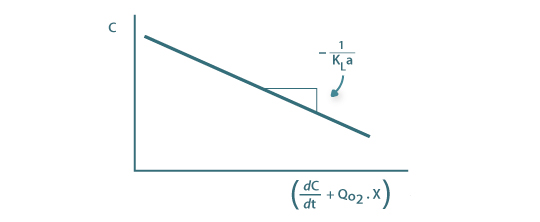
Figura 12: Determinação de KLa pelo método dinâmico (eq. 57)
Esta metodologia requer a determinação de declives na curva de C em função de t (Figura 11) o que pode ser um desafio aliciante mas com indeterminações significativas.
Considerando, porém, que a escala de tempo da experiência é de várias ordens inferior à escala de tempo da fermentação poder-se-á assumir um estado quasi-estacionário entre a transferência e o consumo de oxigénio no momento da experiência, isto é, a concentração média, 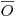 , de oxigénio dissolvido manter-se quasi-estacionária.
, de oxigénio dissolvido manter-se quasi-estacionária.
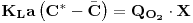 | (58) |
Substituindo esta expressão na equação 55 resulta
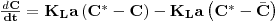 | (59) |
Rearranjando esta equação, obtém-se
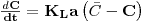 | (60) |
Integrando, resulta
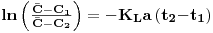 | (61) |
Nota:
- Este é um método não invasivo e, portanto, adequado ao uso com microrganismos.
- É pressuposto que as bolhas não são retidas no interior do fermentador quando para a fase de desarejamento se fecha o fornecimento de ar.
- É apropriado preencher o espaço livre do fermentador (headspace) com N2 a fim de desagregar o efeito de arejamento de superfície.
- O sensor de oxigénio dissolvido deve ser de resposta rápida.
- As concentrações críticas, Ccr, referidas, abaixo das quais se altera a fisiologia microbiana dependem do microrganismo em causa, podendo tomar-se como referência os seguintes valores:
- bactérias e leveduras 5-10 % da saturação
- fungos 10-50 % da saturação
- células vegetais 10-30 % da saturação
iv) Método do Sulfito
Este método é baseado na oxidação do sulfito a sulfato na presença de um catalisador de Cu2+ ou Co2+, de acordo com o esquema seguinte.
O consumo de oxigénio é muito rápido e a sua concentração é praticamente nula quando a concentração do catalisador é da ordem de 10-3 M. Quantificando quimicamente a quantidade sulfito residual obtém-se, por diferença em relação à quantidade original, a quantidade de oxigénio que reagiu e que é igual à quantidade transferida da corrente de ar. Dividindo pelo tempo de durante o qual essa quantidade de oxigénio foi consumida tem-se a quantidade R consumida por unidade de tempo e, daí, KLa = R/C*.
6.2 Correlações para estimativa de KLa
Um dos aspectos mais importantes a considerar nos processos de cultura de microrganismos é a transferência de massa. Muitas correlações para estimar coeficientes de transferência de massa têm sido propostas, porém, com largas margens de erro, até porque geralmente elas são dependentes da escala ou específicas de processos.
As expressões conhecidas da literatura científica indicam que KLa está directamente dependente da potência transmitida ao fluido e do caudal de ar alimentado ao fermentador, podendo, pois, escrever-se
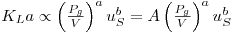 | (62) |
onde us é a “velocidade superficial” do ar:
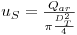 | (63) |
As expressões que têm sido propostas são meramente empíricas. No sistema água-ar em condições de coalescência (soluções salinas, com força iónica elevada) das bolhas e com uma precisão de cerca de 30% pode usar-se a equação
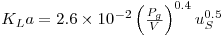 | (64) |
enquanto que em condições de não-coalescência (soluções salinas), como normalmente acontece em sistemas fermentativos se tem
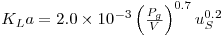 | (65) |
Na equação 62 a constante A é sensível e significativamente diminuída pelos anti-espumas químicos, enquanto que os expoentes a e b variam com a escala de uma modo não específico, o que acarreta problemas na utilização destas expressões em fase de escalamento de dados (scale-up).
7. Majoração de escala (scale-up)
A extrapolação de escala, seja no sentido da majoração (scale-up) seja no sentido da minoração (scale-down) é um problema complexo devido aos múltiplos parâmetros envolvidos e que não permitem obter soluções generalizadas. Assim, diferentes critérios podem ser adoptados, com base em abordagens empíricas, mantendo como denominador comum a “semelhança geométrica” nas escalas consideradas:
- Igual taxa de dissipação de energia específica
- Igualdade de KLa
- Tempos de mistura constantes
- Igual shear
- Igual Número de Reynolds
- Combinação destes ou outros critérios
Contudo a manutenção de semelhança geométrica entre escalas diferentes tem como consequência a dissemelhança cinemática nas diversas escalas.
7.1 Igual taxa de dissipação de energia específica (Pg/V)
Em geral o critério tem sido aplicado considerando os sistemas geometricamente semelhantes nas duas escalas e negligenciando a energia introduzida nos sistemas pelo arejamento forçado (eventualmente não negligenciável).
Considerando então uma escala pequena, representada pelo índice 1, e uma escala grande, representada pelo índice 2, a semelhança geométrica implica que
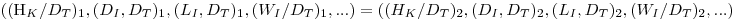
Da equação 45 (P0=5ρNI3DI5) pode escrever-se
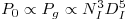 | (66) |
Mantendo a mesma potência por unidade de volume na escala pequena (índice 1) e na escala grande (índice 2), isto é, (Pg/V)1=(Pg/V)2 isso significa que 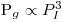 e substituindo na equação tem-se
e substituindo na equação tem-se
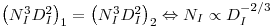 | (67) |
Significa isto que há uma dissemelhança no que respeita à velocidade de rotação do agitador, a qual diminui com o aumento de escala.
As pás do agitador funcionam como uma bomba centrífuga e, considerando o número de arejamento (equação 47) conclui-se que a capacidade de bombagem aumenta com a escala:
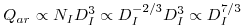 | (68) |
Contudo, a capacidade específica de bombagem, também chamada velocidade de arejamento, diminui ao passar da pequena para a grande escala:
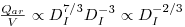 | (69) |
o que se traduz por uma deterioração da qualidade de mistura na grande escala e uma menor velocidade de transferência de massa.
Um factor de grande importância do ponto de vista da fisiologia das células tem a ver com a velocidade de corte, g, a que os microrganismos são sensíveis. A máxima velocidade de corte, gmax, tem lugar na periferia das pás, onde o gradiente de velocidades também é maior. A velocidade linear na periferia das pás, considerando a equação 67, é
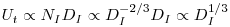 | (70) |
que, assim, aumenta com a escala de onde gmax aumenta com escala. Porém, a velocidade de corte média, 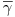 ,
,
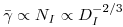 | (71) |
diminui com o aumento de escala, diminuindo também a intensidade de mistura e a velocidade de transferência de massa.
O tempo de circulação é, por definição e pelas equações 39, 47 e 67,
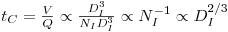 | (72) |
de onde o tempo de mistura que também aumenta com a escala significando menor eficiência da agitação:
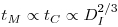 | (73) |
Para que a eficiência de mistura se mantivesse teria que a potência específica de agitação ser maior na grande escala.
Também a velocidade superficial se altera quando se muda de escala, aumentando com a escala:
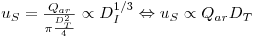 | (74) |
Assim, se se mantiver o caudal por unidade de volume nas duas escalas, a velocidade superficial aumenta mas uS só poderá aumentar até ao ponto de inundação das pás na escala de produção. Se, por outro lado se pretende manter uS nas duas escalas então qualquer estudo em pequena escala (scale-down) deverá ser conduzido a taxas de arejamento (Qar/V) maiores. Deve notar-se que embora (Qar/V) tenha um reduzido efeito em KLa caudais elevados de ar podem causar problemas de espumas e de retenção de ar (hold-up) no fermentador.
7.2 Igualdade de KLa
Se a velocidade de oxigenação for importante para a manutenção de níveis de oxigénio dissolvido então um critério que poderá ser usado será o de manter o mesmo valor de KLa nas duas escalas em consideração. Tendo em conta a relação tipo (equações 62 e 65) para a estimativa de KLa, na hipótese de que os respectivos expoentes não variassem com a escala, e que a velocidade superficial aumenta com a escala quando o número de arejamento é constante, então P0/V (ou Pg/V) necessário para manter uma determinada velocidade de transferência de oxigénio diminui com o aumento de escala. Então, manter o mesmo valor de P0/V (ou Pg/V) pode resultar num sobredimensionamento do motor de agitação a que se adiciona a dificuldade prática de dispor de motores de alta potência para volumes de fermentação elevados.
7.3 Igual Velocidade de Corte (Shear) máxima
Como ficou referido atrás, a velocidade linear da periferia das pás (tip speed) aumenta com a escala (equação 70). O critério de manter a velocidade de corte máxima nas duas escalas poderá ser usado para o scale-up de culturas de micélios, particularmente se não houver um suficiente conhecimento da relação entre a intensidade de corte e da morfologia do micélio. Como regra prática poderá partir-se do princípio de que ocorrerá danificação no micélio para velocidades periféricas superiores a cerca de 3 ms-1, mas factores como a reologia do caldo podem alterar esse valor.
Para a manutenção de Ut no scale-up a potência específica será reduzida o que poderá afectar adversamente a eficiência de arejamento. Um modo de atenuar esta deficiência seria a instalação de mais agitadores de modo a permitir a manutenção de ambos Ut e de Pg/V. Para culturas de bactérias e leveduras este critério é pouco útil.
7.4 Igual tempo de mistura, tM
Se a homogeneidade é importante na resposta da actividade microbiana então o tempo de mistura deve ser mantido de modo a garantir a mesma qualidade de mistura na escala de produção como numa mais pequena escala de teste.
Para fermentadores geometricamente semelhantes a operar em regime turbulento
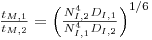 | (75) |
e então assumindo a igualdade de tempos de mistura, resulta
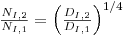 | (76) |
Se, adicionalmente, se Pg/V mantiver igual nas duas escalas (ver a equação 86), então
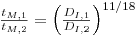 | (77) |
7.5 Igual Número de Reynolds, ReI
A manutenção do ReI nas duas escalas significa que
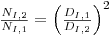 | (78) |
Este critério (assim como a manutenção de outros grupos adimensionais) não funciona em geral para fermentadores, resultando em geral em parâmetros de equipamento e operatórios tecnicamente irrealistas.
7.6 Comparação dos diferentes critérios de escalamento
Cada um dos critérios referidos (e outros não considerados) baseia-se na manutenção de um ou mais parâmetros ao transpor dados e conclusões de uma escala para outra. Porém, outras dissemelhanças são criadas. A manutenção de P/V implica menor velocidade de rotação do agitador, maior velocidade periférica das pás, maior caudal de ar por unidade de volume de liquido, maior tempo de mistura na majoração de escala (scale-up); o valor de KLa também é maior, considerando o caudal de ar por unidade de volume constante ou a velocidade superficial constante. Este poderá ser um critério aplicável quando a oxigenação da cultura é um factor limitativo da eficiência de fermentação. Os critérios de “shear” ou do tempo de mistura, porque implicam um significativo aumento de Pg/V, são pouco realistas, originando heterogeneidades no oxigénio dissolvido e na concentração de nutrientes e dificuldades no controlo do macroambiente. Como foi referido, também a manutenção de ReI não é praticável em sistemas de fermentação. Assim, sendo impossível manter idênticas todas as variáveis características do micro-ambiente deverá o critério de majoração de escala basear-se na(s) propriedade(s) de transporte mais crítica para a eficiência de fermentação.
Nas considerações feitas foi suposto sempre que o fluido (caldo) tinha comportamento Newtoniano. Se os caldos são não-Newtonianos a análise é mais complexa. Também outros factores não foram considerados como a facilidade ou dificuldade de extrair calor de fermentação e manter a temperatura nos valores desejados: estes problemas aumentam com a escala e limitam o factor linear de majoração de escala. Por outro lado, se o fermentador é também usado para esterilizar o caldo, as propriedades reológicas variam com a temperatura e a potência dos motores de agitação também é diferente da que é necessária para a mistura e oxigenação.








