Notação
Bibliografia
Link para internet
Os reactores químicos têm como principal objectivo converter, em condições controladas, reagentes em produtos. A fase de projecto é uma etapa determinante e pode envolver uma série de questões mais ou menos complexas:
- selecção do tipo de reactor;
- obtenção de dados termodinâmicos, leis cinéticas e outras propriedades físico-químicas de reagentes, produtos ou da mistura reaccional;
- selecção das condições operatórias;
- mecanismos de transferência de calor e condições de escoamento;
- projecto mecânico;
- sistemas de controlo e segurança;
- avaliação dos custos de investimento e de produção;
- requisitos de manutenção;
Os “reactores químicos ideais” podem ter subjacente um de dois conceitos básicos, que permitem uma abordagem matemática simplificada destes processos: mistura perfeita, onde se admite que não há variações espaciais das variáveis de estado (composições e temperatura); escoamento pistão (plug flow), onde se consideram as variações espaciais das variáveis de estado (composições e temperatura) na direcção axial do sistema, mas não na direcção radial. No escoamento pistão, admite-se portanto, que os fenómenos de transferência se devem apenas a efeitos convectivos, em que todos os elementos de fluido se movem com a mesma velocidade;
O conceito de mistura perfeita permite a concepção de reactores químicos do tipo:
- reactor contínuo perfeitamente agitado (continuous stirred tank reactor- CSTR);
- reactor descontínuo (batch) perfeitamente agitado;
- reactor semi-descontínuo perfeitamente agitado;
Estes reactores estão representados esquematicamente na Fig.1(a)-(c), sendo possível em algumas situações usar uma associação de CSTR na configuração de bateria de reactores, Fig.1(d). Por oposição, o conceito de escoamento pistão está subjacente aos reactores do tipo tubular (plug flow reactors), Fig.1(e). Na Fig.2(a) colocam-se em evidência os pressupostos de mistura perfeita, para o caso de um reactor contínuo em estado estacionário, onde se processa uma reacção exotérmica. Nestas condições a concentração do reagente i e a temperatura de entrada (Ci0 e T0), decaem para os valores de concentração e temperatura no interior do reactor (Ci e T), que são iguais às condições de saída. Em relação ao reactor tubular do tipo pistão, a Fig.2(b) mostra os perfis axiais, para o caso de estado estacionário, onde se processa uma reacção exotérmica em condições não adiabáticas. Nestas condições, a concentração de entrada do reagente i (Ci0), decai progressivamente ao longo da coordenada axial, Ci(z), até ao valor observado à saída. O perfil temperatura no interior do reactor, T(z), apresenta um ponto quente (hot spot), o qual se localiza na coordenada axial em que a quantidade de calor produzido por reacção química é igual à quantidade de calor transferida para o exterior.
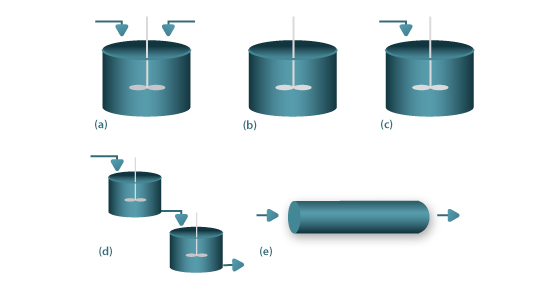
Figura 1- Reactores químicos ideais: (a) Continuous Stirred Tank Reactor (CSTR); (b)- Reactor Descontínuo; (c) Reactor semi-descontínuo; (d)- Bateria de CSTR; (e)- Reactor tubular pistão.
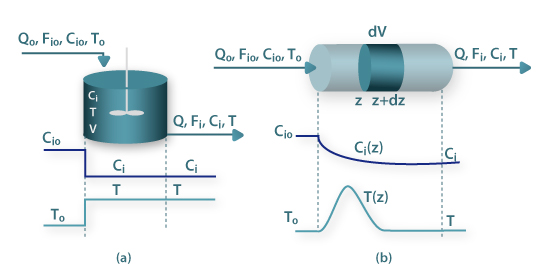
Figura 2- Reactores químicos ideais em estado estacioário: (a) Continuous Stirred Tank Reactor (CSTR); (b)- Reactor tubular pistão.
No caso dos reactores perfeitamente agitados, a transferência de calor com o exterior pode ser promovida com recurso a serpentinas interiores ou camisas externas. Já no caso dos reactores tubulares a transferência ocorre em geral, através da parede lateral para camisas externas.
Projecto de reactores químicos
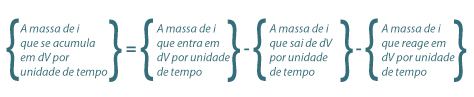
O projecto de reactores químicos é realizado principalmente com recurso a balanços de massa e de energia. Os balanços mássicos podem ser parciais ou globais, e as fronteiras para realizar estes balanços podem corresponder à totalidade do volume do reactor (V) ou a um elemento de volume do reactor (dV), como acontece nos sistema de parâmetros distribuídos. Os balanços de energia podem também considerar a totalidade do volume ou apenas um elemento de volume.
· Reactores químicos perfeitamente agitados
Genericamente, um balanço mássico parcial ao reagente i num reactor perfeitamente agitado, CSTR, pode ser estabelecido como se indica na eq.(1). Esta equação toma a forma matemática indicada na eq.(2), e as unidades de cada termo do balanço são neste caso mol.s-1.
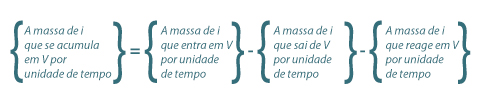 | (1) |
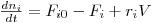 | (2) |
O significado das variáveis da eq.(2) pode encontrar-se na notação. Por outro lado, atendendo a que Fi=QCi, e para uma reacção com uma cinética r=kCin, esta equação pode ser re-escrita na forma:
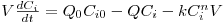 | (3) |
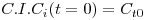 | (4) |
O recurso ao conceito de conversão, xA=(FA0-FA)/FA0, permite analisar o comportamento destes reactores também com base nesta variável de estado, xA. Um parâmetro relevante para os reactores em geral, e para o CSTR em particular é o tempo de passagem, τ, o qual é definido como a razão V/Q. Este parâmetro corresponde ao tempo que o fluido permanece no interior do sistema, e é normalmente determinado de modo a garantir os níveis de rendimento desejados.
A eq.(3) e eq.(4) foram estabelecidas para avaliar o comportamento dinâmico de um reactor do tipo CSTR, esquematizado na Fig.2(a). No entanto, aquelas equações podem facilmente adaptar-se para um reactor descontínuo, se se fizer Q0=Q=0. No caso dos reactores semi-descontínuos, as eq.(3) e (4) também podem ser utilizadas, sendo necessário verificar se Q0 =0 ou se Q=0.
O balanço mássico global ao CSTR pode ser traduzido matematicamente pela equação diferencial indicada na eq.(5),
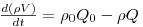 | (5) |
Deste modo, em estado estacionário deve verificar-se que ρ0Q0=ρQ, e no caso em que as massas volúmicas da corrente de entrada e de saída possam ser consideradas iguais (ρ0=ρ) resulta que Q0=Q. Este resultado permite simplificações importantes na análise deste tipo de sistemas.
O balanço energético tem de ser coerente com as leis da termodinâmica, e genericamente pode estabelecer-se de acordo com eq.(6), ou matematicamente como se indica na eq.(7).
 | (6) |
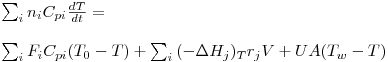 | (7) |
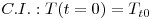 | (8) |
À semelhança do balanço mássico, também o balanço energético indicado na eq.(7) pode ser aplicado ao reactores descontínuos ou semi-descontínuos.
Em termos energéticos os reactores perfeitamente agitados podem operar em condições adiabáticas (quando não há trocas de calor com o exterior) ou não-adiabáticas. Um aspecto relevante na operação deste tipo de sistemas está relacionado com a multiplicidade de estados estacionários, os quais correspondem às condições operatórias em que o calor de reacção, Qr, é numericamente igual ao calor trocado com o exterior, QT. Na prática, devem ser evitadas as condições operatórias que podem conduzir a estados estacionários instáveis.
· Reactores tubulares com escoamento pistão
O escoamento pistão corresponde a uma idealização relativamente ao movimento de fluidos onde se admite que os elementos de fluido se movem com uma velocidade uniforme ao longo de linhas de corrente paralelas, ou seja, não se considera variação radial de velocidade. Deste modo, quando se admite escoamento pistão, o único mecanismo de transferência de calor é a convecção. Esta abordagem permite estabelecer um modelo matemático mais simples, e portanto, mais fácil de resolver.
Genericamente, um balanço mássico parcial ao reagente i num reactor tubular com escoamento pistão pode ser formalizado como se indica na eq.(9), e é estabelecido para o elemento de volume dV (Fig.2(b)). Esta equação pode ser traduzida matematicamente como se indicada na eq.(10), sendo o significado das variáveis o indicado na notação. Uma vez que os balanços são estabelecidos em termos de fluxos mássicos, as dimensões de cada termo são também neste caso mol.s-1.
 | (9) |
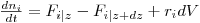 | (10) |
Em estado estacionário, a equação que traduz o balanço mássico parcial é uma equação diferencial ordinária, que necessita apenas de uma condição inicial para ser resolvida:
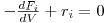 | (11) |
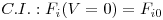 | (12) |
Se o caudal volumétrico poder ser considerado constante, a eq.(11) pode ser re-escrita em termos de concentrações, eq.(13), onde está implícito que dV=Adz :
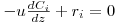 | (13) |
Concretizando para o reagente A, que reage de acordo com uma cinética de primeira ordem, rA=-kCA, e com base no conceito de conversão, CA=CA0(1-xA), o volume do reactor tubular necessário para se atingir uma conversão xA, pode ser calculado por integração da eq.(13):
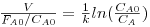 | (14) |
Se no sistema se puder considerar que a temperatura, pressão e o número total de moles são aproximadamente constantes, então o termo V/(FA0/CA0) corresponde ao tempo de residência, τ.
Para os reactores tubulares, o balanço energético também deve ser estabelecido para um elemento de volume, dV, e quando as dimensões de cada termo são J.m-3.s-1, resulta a eq. (15):
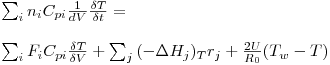 | (15) |
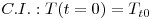 | (16) |
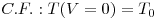 | (17) |
A resolução desta eq.(15) requer o estabelecimento de uma condição inicial, C.I., e uma condição fronteira, C.F. Em estado estacionário, o balanço energético toma a forma indicada na eq.(18), a qual corresponde agora a uma equação diferencial ordinária,
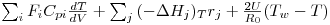 | (18) |
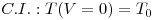 | (19) |
Assim, para se estudar o comportamento ou para o projecto de reactores tubulares com escoamento pistão as eq.(11), (12), (18) e (19) devem ser resolvidas em conjunto como um sistema de equações diferenciais ordinárias. As cinéticas envolvidas no sistema em análise, podem obrigar ao estabelecimento de mais do que um balanço mássico, e em alguns casos resultam sistemas relativamente complexos os quais requerem métodos numéricos e recursos computacionais adequados. Em casos simplificados é possível obter soluções analíticas para o estudo e projecto deste tipo de sistemas.
Indicam-se abaixo algumas referências bibliográficas, que permitem aprofundar o conhecimento sobre reactores ideais.
::: Início :::
Notação
| A | Área de transferência de calor (m2) |
| Ci | Concentração de reagente i à saída do reactor (mol.m-3) |
| Ci0 | Concentração de reagente i à entrada do reactor (mol.m-3) |
| Ci(z) | Concentração de reagente i para a coordenada axial z (mol.m-3) |
| Cpi | Capacidade calorífica molar de i (J.mol-1.K-1) |
| E | Energia de activação ( J.mol-1) |
| F0 | Caudal molar de alimentação (mol.s-1) |
| F0i | Caudal molar do componente i na alimentação (mol.s-1) |
| Fi | Caudal molar do componente i à saída do reactor (mol.s-1) |
| k | Constante cinética (as unidades dependem da ordem da reacção) |
| k0 | Factor de frequência (s-1) |
| L | Comprimento do reactor tubular (m) |
| n | Ordem da reacção do componente i (mol) |
| ni | Moles do componente i (mol) |
| P | Pressão no interior do reactor (Pa) |
| Q0 | Caudal volumétrico da mistura reaccional à entrada do reactor (m3.s-1) |
| R | Constante dos gases perfeitos (J mol-1.K-1) |
| ri | Velocidade da reacção do componente i (mol i. m-3.s-1) |
| rj | Velocidade da reacção j (mol i. m-3.s-1) |
| R0 | Raio interno do reactor tubular (m) |
| T | Temperatura no reactor (K) |
| t | Tempo (s) |
| T0 | Temperatura de alimentação (K) |
| Ti | Temperatura no interior e à saída do reactor no instante inicial (K) |
| ts | Tempo de simulação (min) |
| Tw | Temperatura da parede do sistema (K) |
| U | Coeficiente global de transferência de calor (J.m-2.s-1.K-1) |
| V | Volume do reactor (m3) |
| xA | Conversão do reagente em cada ponto do reactor |
| z | Coordenada axial (m) |
| DH | Calor da reacção (J.mol-1) |
| r | Massa específica da mistura reaccional (kg.m-3) |
| r0 | Massa específica da mistura reaccional à entrada do reactor (kg.m-3) |
| τ | Tempo de passagem ou tempo de residência (s) |
| | | | |
::: Início :::
Bibliografia
- Aris, R., Elementary Chemical Reactor Analysis, Prentice Hall, New Jersey, 1986.
- Cooper, A. R. Jeffreys, G. V., Chemical Kinetics and Reactor Design - Oliver and Boyd, Edinburg, 1979.
- Coulson, J. M., Richardson, J. F., Tecnologia Química, vol. III, Fundação Calouste Gulbenkian, 1982.
- Fogler, H.S. Elements of Chemical Reaction Engineering, 3rd ed., Prentice-Hall, 1999.
- Froment, G., Bischoff, K., Chemical Reactor Analysis and Design, 2nd edition, John Wiley & Sons, 1990.
- Lemos, F. Lopes, J. M. Ramôa Ribeiro, F., Reactores Químicos- Colecção Ensino da Ciência e Tecnologia, IST, 2002.
- Levenspiel, O., Chemical Reaction Engineering, John Wiley & Sons, 3rd ed., 1999.
- Nunes dos Santos, A. M., Reactores Químicos, Fundação Calouste Gulbenkian, Lisboa, 1990.
- Smith, J. M., Chemical Engineering Kinetics, 3rd edition, McGraw-Hill, 1981.
- Villermaux , J., Génie de la Reaction Chimique - Conception et Fonctionnement des reacteurs, Tec & Doc, 1993.
::: Início :::
Link na Internet
http://www.engin.umich.edu/~cre/
::: Início :::








