Transferência de Massa

O que é a TRANSFERÊNCIA DE MASSA? Como ocorre?
2.1 Leis de equilíbrio entre fases
2.2 Difusão molecular
2.3 Transferência de massa por convecção
2.4 Algumas aplicações de transferência de massa
2.5 Transferência de massa através de interfaces
2.6 Correlações empíricas
2.7 Perfis de concentração temporais e/ou espaciais
2.8 Semelhanças entre processos de transferência
2.9 Bibliografia

O que é a TRANSFERÊNCIA DE massa? Como ocorre?

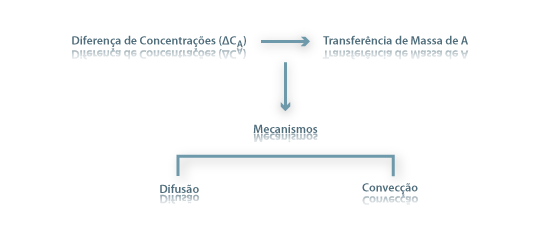
A transferência de massa em sentido lato poderá ser entendida como o movimento espacial da matéria. Como exemplos, refira-se o movimento de um fluido numa conduta ou em torno de corpos. No entanto, “transferência de massa” é geralmente entendida no seu sentido mais estrito, referindo-se ao movimento de um componente específico (A, B…) num sistema de vários componentes. Existindo regiões com diferentes concentrações, ocorrerá transferência de massa no sentido das zonas onde a concentração desse componente é mais baixa. Essa transferência pode ocorrer pelo mecanismo da difusão molecular ou da convecção . Recorde-se que a concentração é geralmente definida como a quantidade de substância (em moles ou massa) por unidade de volume ([C_A]=mol.m^-3; [ρ_A]=kg.m^-3 sendo ρ_A=C_A.M_A em que M_A é a massa molar de A). Em gases perfeitos, a concentração de cada gás individual pode ser calculada a partir da sua pressão parcial, p_A: C_A=p_A/(R.T), onde T é a temperatura absoluta (K) e R a constante dos gases perfeitos (8,314 J.mol^-1.K^-1). Da mesma forma, a concentração total de todas as espécies (C) está relacionada com a pressão total, P na forma C=P/(R.T). Por sua vez, a fracção molar de um componente A numa mistura é o quociente entre o número de moles de A, n_A, e o número total de moles, n_total, isto é, x_A=n_A/n_total e y_A=n_A/n_total, num líquido e num gás, respectivamente. Num gás a fracção molar pode ser relacionada com a pressão parcial através da lei de Dalton y_A=p_A/P e é também igual à percentagem volumétrica (%V/V). Por exemplo, existindo 20% (V/V) de NH₃ no ar, então y_NH3=0,2.

Muitas ocorrências do dia-a-dia envolvem transferência de massa: processo de solubilização de açúcar no chá, favorecido pela agitação de uma colher, solubilização de sal em água, preparação de um chá por infusão (Fig.11), evaporação de água na superfície de uma piscina e transporte através do ar envolvente, secagem de um tronco de madeira após o corte e correspondente transporte da humidade através dos poros da madeira até à sua superfície, solubilização de oxigénio em água num aquário para consumo dos peixes, arejamento de reservatórios de água, solubilização de oxigénio num meio nutriente para consumo de microorganismos num processo de fermentação aeróbia, transferência de reagentes para a superfície de um catalisador, onde ocorre uma reacção…

Figura 11: Preparação de chá por infusão (extracção sólido/líquido seguido de difusão). O processo de transferência de massa é favorecido pela agitação da colher (convecção).

 ::: Início :::

2.1 Leis de equilíbrio entre fases

A transferência de massa através de uma fase ou entre duas fases passando a fronteira entre elas (líquida-líquida, líquida-sólida, gás-líquida ou gás-sólida) requer um afastamento das condições de equilíbrio. Por exemplo, poder-se-á dissolver sal numa panela com água até a concentração de sal na água atingir o valor máximo, designado por solubilidade, a qual depende da temperatura da água. Outro exemplo, é a secagem da roupa, que ocorrerá mais rapidamente se o ar estiver mais seco (isto é, quando a pressão parcial de vapor de água no ar estiver mais afastada do seu valor máximo, sendo este dado pela pressão de vapor correspondente à temperatura considerada). Os valores das concentrações de equilíbrio entre fases (C_A^F1, C_A^F2, respectivamente na fase 1 e fase 2) são apresentados na literatura sob variadas formas: tabelas, gráficos, coeficientes de distribuição ou partição e equações do tipo C_A^F1=m.C_A^F2. Nalguns casos é possível obter uma expressão analítica simples como os equilíbrios líquido-gás descritos pela Lei de Henry, válida para misturas diluídas (eq. 19), ou os descritos pela lei de Raoult (eq. 20) onde p_A é a pressão parcial do componente A na mistura gasosa em equilíbrio com o líquido cuja concentração em A é C_A:

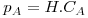
(lei de Henry, com [H]=Pa.m3/mol ou J/mol)

(19)

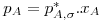
(lei de Raoult com xA=CA/C, sendo p*A,σ a pressão de vapor de A puro e C a concentração total - válida para misturas ideais)

(20)

As figuras 12 a 14 ilustram situações onde ocorre transferência de massa, mostrando a forma de calcular o valor da concentração do componente A na fronteira entre fases (dado pelo valor de equilíbrio).

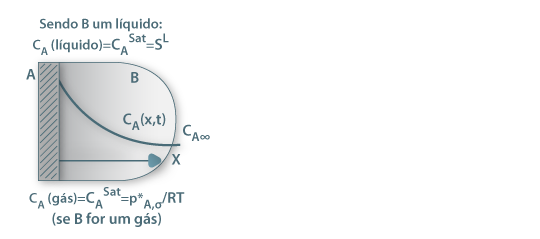
Figura 12: Solubilização de A (sólido) num líquido B ou sublimação de A num gás B. A concentração de A à superfície é dada pela solubilidade (S^L) e pressão de vapor (p^*_A,σ), respectivamente.

Figura 13: Solubilização de A (gás) num sólido B. A concentração de A no sólido, junto da superfície é dada pela solubilidade [S]=mol/(m³ sólido.Pa); [C_AS]=mol/(m³ sólido).

Figura 14: Absorção de um gás soluto A num líquido B. Se A for pouco solúvel em B (solução diluída) é, em geral, aplicável a Lei de Henry e C_AS(líquido) =C_Ai^L=ρ_Ai^G/H, [H]=Pa.m³/mol ou J/mol.

 ::: Início :::

2.2 Difusão molecular

A transferência de massa por difusão molecular em consequência de uma diferença de concentrações espacial é análoga à transferência de calor por condução embora seja um fenómeno mais complexo pois ocorre numa mistura com pelo menos duas espécies químicas. Começando com o caso dos gases, o estabelecimento da igualdade de concentrações ao fim de um determinado tempo resulta do movimento molecular aleatório em todas as direcções do espaço (este movimento de natureza estatístico é explicado pela teoria cinética dos gases a baixas pressões). Na Fig. 4 está representado um recipiente dividido por uma placa de área A; uma das partes contém moléculas A e B enquanto a outra divisão só contém moléculas B, sendo C_A=0 mol/m³. Se a placa que divide o recipiente for retirada, o movimento molecular aleatório permite que moléculas A e B possam frequentar o espaço anteriormente definido por V2. Contudo, a probabilidade de uma molécula A entrar nesse espaço é maior do que a de sair do mesmo, uma vez que aí a sua concentração inicial era 0. Ao fim de algum atempo, todo o espaço conterá moléculas A e a concentração será uniforme.

A velocidade de transferência de massa do componente A (mol de A/s) num meio em repouso contendo uma mistura binária A e B é proporcional à área de transferência perpendicular ao movimento (A) e ao gradiente de fracções molares (dx_A/dz), sendo conhecida pela 1ª lei de Fick (eq. 21). A constante de proporcionalidade é designada por difusividade mássica ou coeficiente de difusão de A no meio B (D_AB, m²/s) que tem as mesmas unidades da difusividade térmica α apresentada na secção de transferência de calor. 

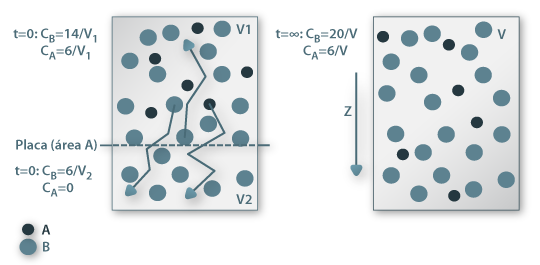
Figura 15: Difusão do componente A num recipiente após a remoção de uma placa que o divide em duas secções.

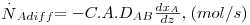
(21)

Se a concentração total (C, moles de (A+B)/m³) for constante, ou aproximadamente constante como em soluções diluídas,

 

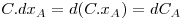
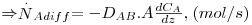
(22)

 Cuja integração, no caso de gases, resulta em:

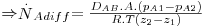
(23)

Onde p_A1 e p_A2 são, respectivamente, as pressões parciais de A mantidas constantes nas fronteiras z₁ e z₂ (isto é, nos extremos do percurso de difusão), considerando o gás como perfeito (C_A=p_A/(RT)).

No caso de difusão em líquidos e sólidos é comum usar, por analogia, equações idênticas à eq. 23 (usando, obviamente, concentrações em vez de pressões parciais).

Numa mistura gasosa binária, o coeficiente de difusão D_AB = D_BA ~10^-5 m²/s sendo dependente da temperatura e da pressão na forma geral D∝T^2/3/P (como previsto pela teoria cinética dos gases). Em líquidos, a velocidade de difusão molecular é menor pois as moléculas estão mais próximas, aumentando as colisões e a resistência à difusão. Assim, D_AB depende da concentração de A em B e toma valores ~ 10^-9 m²/s; globalmente, D_sólidos ≤ D_líquidos « D_gases. Se a área de transferência de massa for constante é comum associá-la à velocidade molar, obtendo-se o fluxo molar (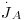, em mol.m^-2.s^-1):

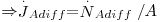
 ::: Início :::

2.3 Transferência de massa por convecção

O mecanismo de transferência de massa através de um fluido em movimento é designado por convecção sendo esta natural (se o movimento for provocado por diferenças de densidades) ou forçada (se o movimento for provocado por acção de agentes externos, como uma ventoinha, bomba centrifuga, ou outros).

Considere-se uma mistura binária (A+B) a deslocar-se devido a diferenças de pressão, como um fluido a escoar no interior de uma conduta (figura 16). Se não houver gradientes de concentração, a velocidade média de deslocamento do componente A é igual à velocidade média molar do fluido e a velocidade de difusão molecular prevista pela 1ª lei de Fick é nula (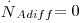). Contudo, se houver gradientes de concentração, um observador exterior verá que a velocidade de deslocamento de A será maior que a velocidade média do fluido uma vez que A se vai difundir no sentido do gradiente negativo. Assim, a velocidade de transferência de A (mol A/s) é o resultado da contribuição do movimento convectivo (devido ao movimento global do fluido) e do movimento difusivo (devido ao gradiente de concentrações, dado pela 1ª lei de Fick) – eq. 24.

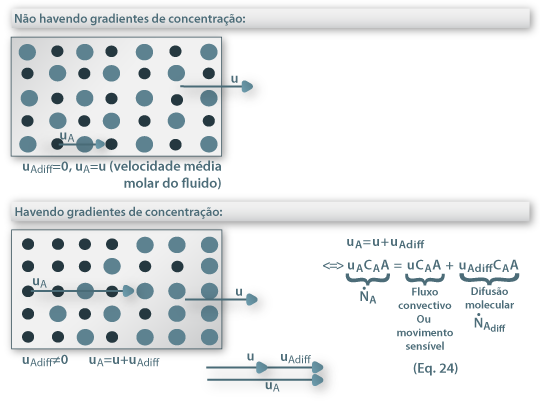
Figura 16: Representação do processo de transferência de massa de A na ausência de variações espaciais de concentração (escoamento global de um fluido) ou na presença destas.

Sendo a velocidade total de transferência de massa 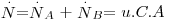, retirando o valor da velocidade média molar u e substituindo-a na eq. 24 obtém-se a eq. 25 que, rearranjada, dá lugar à eq. 26, conhecida como a equação geral da difusão:

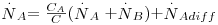
(25)

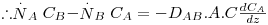
(26)

Existem casos em que o fluxo de B é nulo, como, por exemplo, se um gás B for muito pouco solúvel num líquido A, e o vapor A se difundir através de B  – é o caso da evaporação de água no ar ou da absorção de amoníaco em água a partir de uma mistura gasosa. Nestes casos, a integração da eq. 26 dá origem à eq. 27:

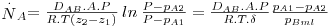
(27)

No entanto, quando o fluxo de A é igual mas em sentido contrário ao de B como em alguns processos de destilação (N_A = -N_B, denominada contradifusão molecular), ou ainda para misturas diluídas (líquidas ou gasosas) e na transferência de massa através de sólidos, em que p_Bml ≈P (pressão total) ou C_Bml ≈ C (concentração total), a eq. 27 resume-se à equação de Fick (eq. 23).

Em muitos casos, o escoamento é turbulento sendo caracterizado pela formação de turbilhões que se movimentam rápida e aleatoriamente. Estes turbilhões ou “pacotes” de fluido permitem transportar as moléculas A, por exemplo de um sólido que se dissolve num líquido, em maior quantidade e rapidez do que a difusão molecular. Assim, poder-se-á escrever a eq. 24 na forma

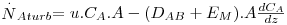
(28)

Figura 17: Evaporação ou sublimação no seio de um fluido em movimento.

em que E_M é a difusividade turbilhonar sendo esta dependente do padrão de escoamento do fluido e variável com a posição (toma o valor zero junto à superfície e aumenta com a distância à parede). Como geralmente E_M não é conhecido, bem como a profundidade z , é comum definir um coeficiente de transferência de massa, k_G,L, à semelhança da definição de coeficiente de transferência de calor. Este coeficiente leva o índice G quando a transferência é efectuada no seio de um gás e o índice L quando se trata de um líquido, e depende da geometria da superfície, das propriedades do fluido e das condições de escoamento do fluido.

Assim, a velocidade de transferência de massa será obtida através da eq. 29 sendo A, a área de transferência de massa perpendicular ao fluxo de massa, e ΔC_A a driving-force, isto é, a causa para ocorrer a transferência de massa (p.e. pode ser (C_AS-C_A∞) em que C_AS é a concentração de A junto à superfície e C_A∞ é a concentração de A no fluido que a envolve - Fig. 18). Consoante se trate de um gás ou de um líquido, poder-se-á definir outros coeficientes de transferências de acordo com as driving-forces consideradas – eq.30 a 32.

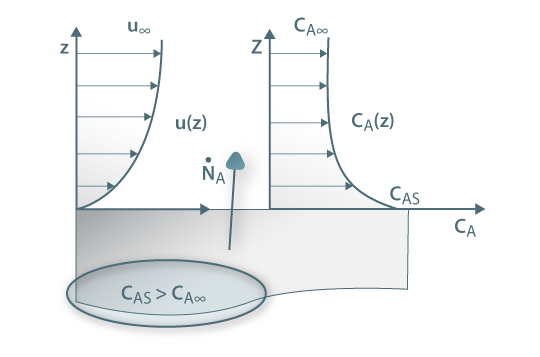
Figura 18: Transferência de massa no seio de um fluido em movimento – perfis de velocidade e concentração.

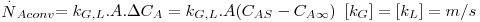
(29)

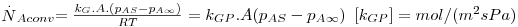
(30)

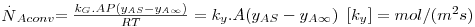
(31)

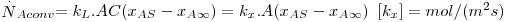
(32)

Comparando a eq.30 com a equação 27, e re-arranjando, conclui-se que

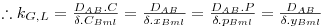
(33)

no caso de contradifusão molecular ou misturas diluídas (eq.23),

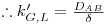
(34)

 ::: Início :::

2.4 Algumas Aplicações de Transferência de massa

 

a) Difusão de A através de corpos porosos

Em sólidos porosos com os poros cheios de fluido (p.e. catalisadores) o movimento sensível é desprezável, pelo que é válida a lei de Fick. No entanto, como mostra a figura 19, o percurso real de difusão é superior à espessura do sólido, sendo o percurso effectivo Z_eff=τ(z₂-z₁) onde τ é a tortuosidade (para sólidos inertes τ =1,5 a 5 ). Sendo ε a porosidade do sólido, virá, por integração da Eq. 22:

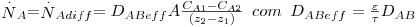
(35)

Para muitos catalisadores granulados, em que o fluido é gasoso, o coeficiente de difusão efectivo do componente A no interior do catalisador é 10 vezes mais pequeno do que o coeficiente de difusão de A no exterior (D_eff ≅ (1/10) D_{fluido livre}).

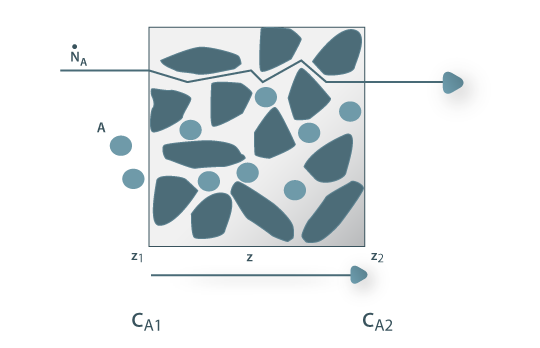
Figura 19: Difusão de A através de um corpo poroso.

b) Difusão de A através de membranas (M)
Considere-se dois fluidos (F1 e F2) separados por uma membrana (como, por exemplo, a parede de um tubo de diálise). Através de uma membrana o movimento sensível é também desprezável, pelo que é aplicável a lei de Fick. Por integração da Eq. 22, obtém-se, atendendo às condições fronteira definidas na Fig. 20:

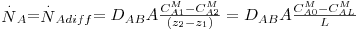
(36)

Se a área de transferência for constante, atendendo à lei de equilíbrio apresentada na Fig. 20 e definindo Permeabilidade da membrana (m².s^-1) P_M=m.D_AB, o fluxo molar será

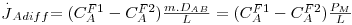
(37)

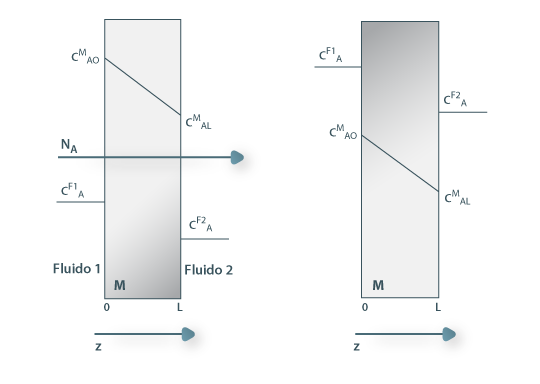
Figura 20: Difusão de A através de uma membrana a descontinuidade dos perfis (isto é, a relação entre a concentração de A dentro e fora da membrana) depende da lei de equilíbrio: C_Ai^M₌ m.C_A^fluido podendo m ser superior à unidade (como na imagem da esquerda), igual a um, ou inferior à unidade (como na imagem da direita).

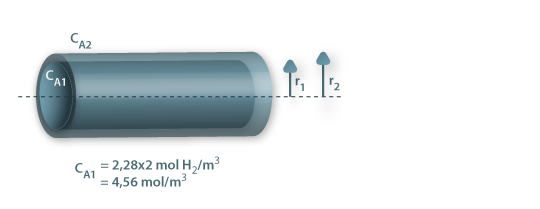
c) Exemplo de aplicação: difusão de H₂ através da parede de um tubo cilíndrico
Um tubo de borracha (neopreno vulcanizado), com 3,0 mm de diâmetro interno, 11 mm de diâmetro externo, e 1 m de comprimento é utilizado para transportar hidrogénio gasoso a 2 atm e 27 ºC.

a) Calcule a perda de hidrogénio através da parede de borracha, em mol/h.
b) Discuta como varia essa perda com as condições de pressão e temperatura do hidrogénio.

A solubilidade do hidrogénio na borracha a 27ºC é S = 2,28×P mol H₂/m³ de sólido, onde P é a pressão do hidrogénio gasoso em atm. A difusividade do hidrogénio na borracha a 27ºC é 1,8×10^-10 m²/s.

Pressupostos: condições estacionárias; simetria cilíndrica; N_B=0 e fluxo convectivo desprezável, pelo que é aplicável a lei de Fick (eq. 22); concentração de H₂ no exterior é ≈0.

 

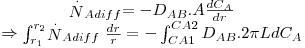
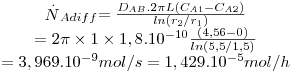
 ::: Início :::

2.5 Transferência de massa através de interfaces

Considere-se novamente o caso de dois fluidos separados por uma membrana, como mostra a Fig. 21, conhecendo-se a concentração do componente A, ou soluto, em ambos os fluidos (C_∞1 e C_∞2); junto à superfície da membrana as concentrações são respectivamente C^F_S1 e C^F_S2, enquanto no interior da membrana, também junto à superfície, são C^M_S1 e C^M_S2. À transferência de massa do soluto A estão associadas três resistências mássicas em série, correspondentes à convecção através do fluido mais concentrado, à difusão através da membrana e à convecção através do fluido menos concentrado. Esta situação é análoga a uma já apresentada anteriormente onde ocorria transferência de calor, como ilustrado na Fig.21 e Tabela 4.

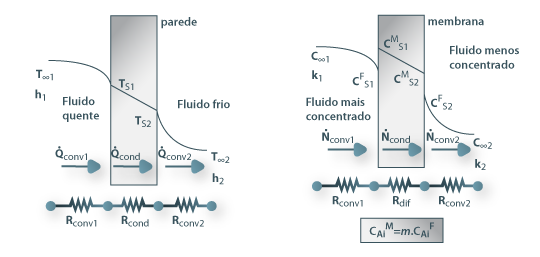
Figura 21: Analogia entre resistências térmicas em série e resistências mássicas em série.

Tabela 4 – Analogia entre os processos de transferência de calor e de massa ilustrados na Fig21

Aplicando as Eq. 29 e 22, obtém-se:

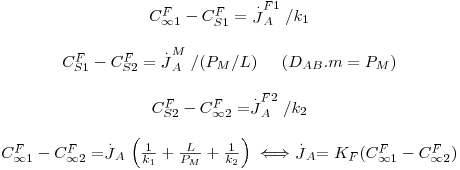
(38)

sendo K_F o coeficiente global de transferência de massa. Neste portal, na secção de “Processos Biológicos/Processos de Separação/Membranas”, são exemplificadas algumas aplicações envolvendo membranas .

Seguindo o mesmo raciocínio, pode-se estabelecer o coeficiente global de transferência de massa para o caso da transferência de um soluto A de uma fase gasosa, G, para uma fase líquida, L, como acontece no processo de Absorção. Este caso será mais desenvolvido na secção “Absorção” deste portal.

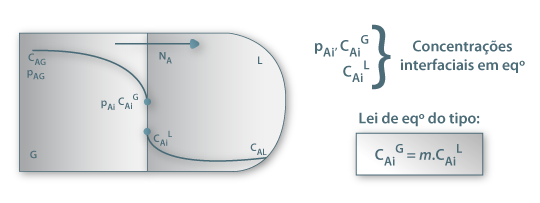
Figura 22: Absorção de A contido num gás G por meio de um líquido L.

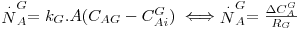
(39)

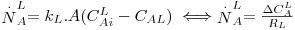
(40)

multiplicando a Eq. 40 por m, ter-se-á:

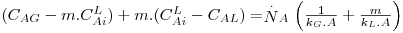
(41)

definindo agora K_G pela Eq. 42 e comparando-a com a Eq. 41, tem-se, finalmente:

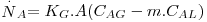
(42)

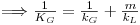
(43)

onde K_G (m/s) representa o coeficiente global de transferência de massa baseado na diferença de concentrações entre duas fases gasosas, uma real, de concentração C_AG e outra fictícia cuja concentração é m.C_AL.

Em vez de multiplicar a Eq. 40 por m, poder-se-ia multiplicar a Eq. 39 por 1/m, obtendo-se:

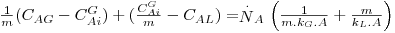
(44)

definindo K_L pela Eq. 45 e comparando-a com a Eq. 44, obtém-se:

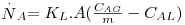
(45)

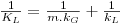
(46)

 sendo K_L (m/s) o coeficiente global de transferência de massa baseado na diferença de concentrações entre duas fases líquidas, uma fictícia de concentração C_AG/m e outra real de concentração C_AL. Comparando a Eq. 46 com a Eq. 43, conclui-se que

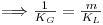
(47)

 ::: Início :::

2.6 Correlações empíricas

Tal como no caso de transferência de calor , também é comum agrupar as variáveis associadas aos processos de transferência de massa sob a forma de números adimensionais e estabelecer correlações entre eles usando dados experimentais. Os coeficientes de transferência de massa dependem das propriedades físicas do fluido (viscosidade, μ, massa volúmica, ρ, coeficiente de difusão, D_AB), da sua velocidade, u, e das dimensões da superfície por onde este se escoa, sendo L a sua dimensão característica: k_G,L=f(μ, ρ, D_AB, u, L).

Usando uma técnica de análise das dimensões das várias variáveis, é possível obter os números adimensionais característicos de um processo de transferência de massa por convecção forçada:
- o número de Reynolds, Re=ρ.u.L/μ que caracteriza o escoamento do fluido
- o número de Schmidt, Sc=μ./(ρ.D_AB) que relaciona propriedades físicas do fluido
- o número de Sherwood, Sh=k_G,L.L/D_AB que representa o aumento da transferência de massa como resultado do movimento do fluido (“convecção”) relativamente à transferência de massa apenas ao nível molecular (difusão)

Existem ainda outros números adimensionais possíveis que resultam da combinação destes:
- o número de Stanton para transferência de massa, St_m = Sh/(Re.Sc)= k_G,L./u
- o número de Peclet para transferência de massa, Pe_m = Re.Sc = u.L/D_AB
- o factor de Colburn, j_D=St_m. Sc^2/3 = (k_G,L./u).Sc^2/3

Seguem-se alguns exemplos de correlações empíricas para o cálculo do coeficiente de transferência de massa. 

- Escoamento de fluidos em torno de esferas

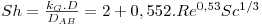
válida quando o fluido é gasoso e 1<Re<48000; 0,6<Sc<2,7; notar que Sh→2 quando u→0.

No caso de líquidos:

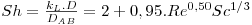Se 2<Re<2000

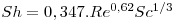Se 2000<Re<17000

 ::: Início :::

2.7 Perfis de concentração temporais e/ou espaciais

Quando a concentração do componente A de uma mistura binária (A e B) varia no tempo (regime não estacionário, ou transiente) ou no espaço por haver produção interna do componente A por reacção química (R_A - velocidade de produção de A/volume, mol A.m^-3.s^-1), ou ainda quando este é consumido por reacção química, é necessário efectuar um balanço molar ao componente A num volume diferencial dV=dx.dy.dz, como mostra a figura 23, para conhecermos a evolução espacial e/ou temporal da sua concentração. Neste portal, na secção de “Reacção Química ”, são exemplificados processos que envolvem reacção e onde estes assuntos são mais aprofundados.

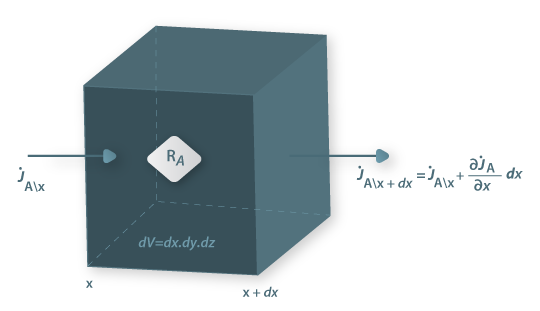
Figura 23: Volume de controlo diferencial no interior do qual ocorre uma reacção química que envolve o componente A.

Aplicando a lei da conservação da massa para a espécie A (moles) no intervalo de tempo dt e considerando haver transporte de A apenas na direcção x:

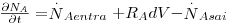
(48)

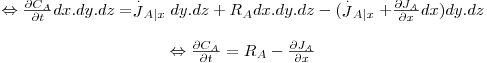
(49)

 sendo

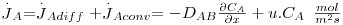
(50)

A eq. 49 descreve genericamente um processo de transferência de massa unidireccional em regime transiente. Existindo variação da concentração de A no tempo (regime transiente) e no espaço, é necessário, para resolver estas equações diferenciais, conhecer uma condição inicial (para t=0) e duas condições fronteira (visto haver uma derivada de 2ª ordem em x). Existem soluções analíticas para geometrias simples e condições fronteira simples, que permitem conhecer os perfis temporais e espaciais da concentração de A. Essas soluções envolvem as variáveis x (distância genérica), L (metade da espessura da placa), t (tempo), D_AB (difusividade mássica de A em B), C_A0 (concentração do componente A no interior do volume de controlo para t=0), C_AS (concentração de A na fronteira do corpo) ou C_A∞ (concentração de A no fluido envolvente do corpo). Para reduzir o número de parâmetros utilizam-se números adimensionais, tais como os apresentados na tabela 5.

Tabela 5 – Números adimensionais associados a processos de transferência de massa em estado transiente e/ou onde ocorre reacção química.

	Nº adimensional
concentração adimensional		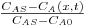CA(x,t) – concentração de A no corpo (função da distância e do tempo)
distância adimensional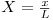
tempo adimensional (número de Fourier para transferência de massa)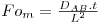
Módulo de Thiele		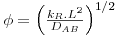kR – constante cinética, s-1
Número de Biot para transferência de massa		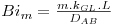CAF=m.CAS

 

a) caso da difusão unidimensional de pequenas quantidades de A através de B na ausência de reacção química (R_A=0) e de movimento sensível (u=0) com D_AB constante (2ª lei de Fick)

Substituindo a eq.50 na 49, obtém-se, respectivamente para coordenadas cartesianas, cilíndricas e esféricas:

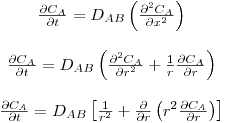
(51)

Para qualquer sistema de coordenadas e várias dimensões, a expressão genérica 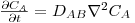é

e 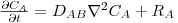no caso de haver reacção.

A solução da eq. 51 é uma série infinita, sendo o 1º termo o mais significativo se Fo>0,2:

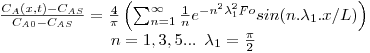(52)

 Após o tempo t_F, a concentração média na placa é dada por:

 

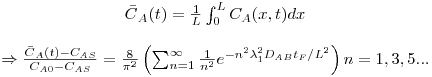
A figura 24 mostra a variação da concentração média de A no interior da placa ao longo do tempo, quando a superfície da placa sobre uma alteração brusca de concentração desde C_A0 (t=0) para o valor de C_AS. Para comparação são igualmente representadas na mesma figura as evoluções temporais no caso das geometrias cilíndrica e esférica. Como se pode ver, a forma esférica é a que permite maior rapidez na evolução dessa concentração.

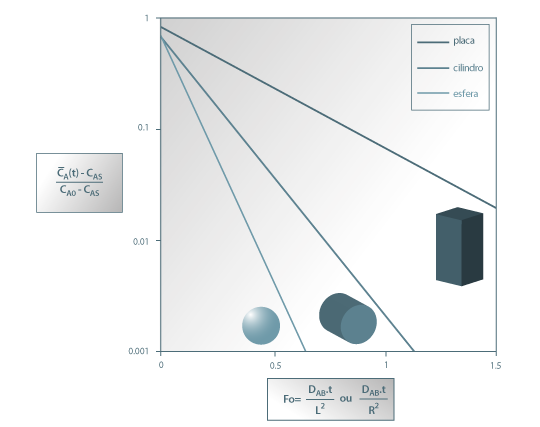
Figura 24: Evolução da concentração média espacial de A ao longo do tempo – comparação entre três formas geométricas (placa, cilindro infinito e esfera).

b) caso da difusão de A unidimensional num meio homogéneo onde ocorre reacção química de 1ª ordem, irreversível (R_A= -k_R.C_A), em estado estacionário, na ausência de movimento sensível e sendo D_AB constante.

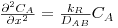  C_A=C_AS para x=0 ; dC_A/dx=0 para x=L (eixo de simetria)

 

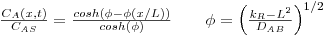
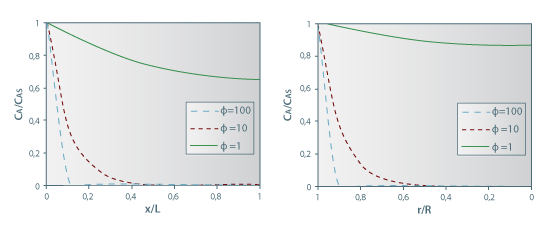
Figura 25: Evolução espacial da concentração de A para diferentes valores do módulo de Thiele (simetria plana, à esquerda, e esférica, à direita).

A figura 25 mostra a evolução espacial da concentração de A para diferentes valores do módulo de Thiele. Quando a velocidade da reacção é elevada (por exemplo, Φ=100) o componente A é totalmente consumido a uma curta distância da fronteira (x/L=0,1), ao contrário do caso em que a reacção é lenta (por exemplo, Φ=1).

c) Difusão radial de A através dos poros de um catalisador esférico onde ocorre reacção química de 1ª ordem (R_A= -k_R.C_A), em estado estacionário, na ausência de movimento sensível e sendo D_eff constante

 

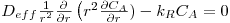
C_A=C_AS para r=R ; dC_A/dr=0 para r=0

A solução é:

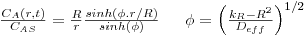
A figura 25 mostra, também para este caso, a evolução espacial da concentração de A para diferentes valores do módulo de Thiele. Na secção de “Reacção Química ”, são apresentados casos de aplicação destes processos que envolvem reacção.

d) Exemplo de aplicação:

Uma placa sólida porosa de agar (gel) a 278 K, com 10 mm de espessura, contém uma concentração uniforme de ureia igual a 0,1 kmol/m³. A placa é subitamente imersa em água pura agitada de tal forma que a resistência superficial à transferência de massa possa ser desprezada (k_L→∞). A difusividade da ureia em agar é 4,72×10^-10 m²/s. Supondo que a difusão ocorre na direcção perpendicular às faces de maior área, e que as concentrações de um lado e de outro da interface água/agar são iguais, desenhe o perfil de concentração de A após 10h.

Aplica-se a eq. 52, considerando apenas o 1º termo da série (o erro cometido é pequeno se Fo>0,2) e sendo C_AS=0 e C_A0=100 mol/m³:

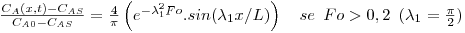
O perfil de concentrações está representado na Figura 26.

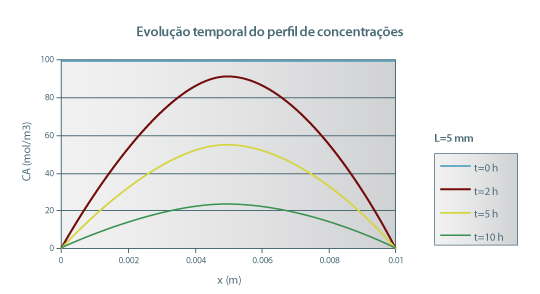
Figura 26: Evolução temporal do perfil de concentrações de ureia numa placa de agar com 10 mm de espessura, colocada em água pura para t=0.

 ::: Início :::

2.8 Semelhanças entre processos de transferência

Os vários Processos de Separação existentes, não só com a finalidade de purificar correntes mas também para produzir compostos, podem ser agrupados quanto ao processo de transferência predominante: transferência de quantidade de movimento, transferência de calor e transferência de massa. Nalguns, como a secagem, ocorre mais do que um processo de transferência em simultâneo (Fig.27). Operações que envolvem transferência de quantidade de movimento são, por exemplo, o escoamento de fluidos, o processo de mistura, a sedimentação, ou a filtração. Como operações que envolvem transferência de calor pode-se referir a transferência de calor nos permutadores de calor, a evaporação, a destilação, a secagem. Como exemplo de operações que envolvem transferência de massa, refira-se a destilação, a secagem, a absorção, a extracção, a adsorção, os processos com membranas.

Os três processos são caracterizados pelo mesmo tipo de equação geral:

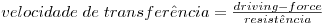
A Tabela 6 mostra as semelhanças entre os diferentes processos, respectivas driving-forces e equações básicas.

Tabela 6 – Semelhanças entre os processos de transferência.

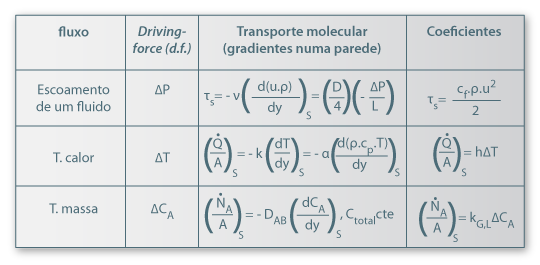
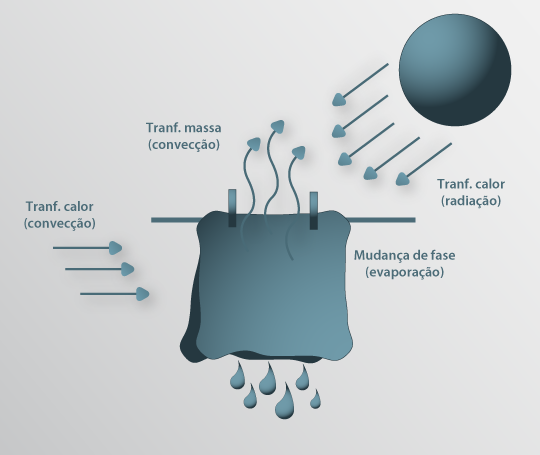
Figura 27: Processo de secagem de roupa, mostrando os diversos processos de transferência e respectivos mecanismos.

 ::: Início :::

Bibliografia:

R. B. Bird, W. E. Stewart, E. N. Lightfoot, "Transport Phenomena", revised 2nd ed., John Wiley & Sons, Inc., New York, 2007

Y.A. Çengel, “Heat Transfer: A practical approach” McGraw-Hill Inc., N.Y. , 2nd ed 2003.

J.P.Holman, “Heat Transfer” 9th ed. , McGraw-Hill Inc., N.Y. , 2002.

F.P. Incropera, D.P. de Witt, “Fundamentals of Heat and Mass Transfer”, 5th ed., J. Wiley & Sons, N.Y. , 2002.

J. M. Kay & R. M. Nedderman, "Fluid Mechanics and Transfer Processes", Cambridge University Press, Cambridge, 1985.

J.R. Welty, C.E. Wicks, Rorrer, R.E.Wilson, “Fundamentals of momentum, heat and mass transfer”, 5th ed. John Wiley &Sons, Inc; N.Y., 2008.

http://www.cheresources.com/convection.shtml

 ::: Início :::